Keplersche Fassregel

Die Keplersche Fassregel (nach Johannes Kepler) ist eine Methode zur näherungsweisen Berechnung von Integralen. Der Magistrat der Stadt Ulm, wo die Rudolfinischen Tafeln gedruckt wurden, beauftragte Kepler, neue Maßeinheiten für die Stadt festzulegen. Solche praktischen Probleme des Handels hatte er schon mehrfach zuvor mathematisch gelöst. Unter anderem beschrieb er in der Nova Stereometria doliorum vinariorum von 1615 eine Methode zur Berechnung der Kapazität von Weinfässern mit unregelmäßigen Formen:

Ist f(x) die Parabel durch die drei Punkte:

${\Big (}a;f(a){\Big )},\;{\Big (}b;f(b){\Big )},\;{\Big (}{\frac {a+b}{2}};f{\big (}{\frac {a+b}{2}}{\big )}{\Big )}$

so ist die Fläche unter der Parabel gegeben durch:

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „http://localhost:6011/de.wikipedia.org/v1/“:): {\displaystyle A=\frac{b-a}{6} \cdot \left( f(a)+4 \cdot f\! \left( \frac{a+b}{2} \right) + f(b) \right)}

und berechnet eine Näherung für

I=\int _{a}^{b}f(x)\,\mathrm {d} x

Beispiele:

Kreisfläche: $A_{Kreis}={\frac {2R}{6}}\cdot (0+4\cdot 2R+0)={\frac {8R^{2}}{3}}=2.67\cdot R^{2}$ Datei:Fassregel1.gif

Die Kreisfläche wird zu klein berechnet, weil der Halbkreis durch eine Parabel angenähert wird; der genaue Näherungswert ist $3.14\cdot R^{2}$ . Es wäre hier besser, die Simpsonregel zu verwenden.

Fläche unter der Sinuskurve $f(x)=sin(x)$ von 0 bis $\pi$

$A_{Sinuskurve}={\frac {\pi }{6}}\cdot (0+4\cdot 1+0)={\frac {4\cdot \pi }{6}}={\frac {2\cdot \pi }{3}}=2.09$

$I=\int _{0}^{\pi }(sin(x))\,\mathrm {d} x=2$

Datei:Fassregel2.gif

Der genaue Wert des Flächeninhalts ist 2 Flächeneinheiten. Die Näherung ist recht gut.

Fläche unter der Parabel $f(x)=-x^{2}+1$

$A_{Parabel}={\frac {2}{6}}\cdot (0+4\cdot 1+0)={\frac {4}{3}}=1.33$

$I=\int _{-1}^{1}(-x^{2}+1)\,\mathrm {d} x=1.33$

Datei:Fassregel3.gif

Die Fläche wird mit der Fassregel richtig berechnet.

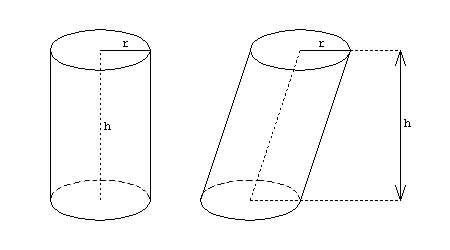
Der Name Fassregel lässt sich durch die folgende Anwendung motivieren: Zur Berechnung des Volumens eines Weinfasses sei $q(x)$ die Querschnittsfläche quer zur Längsachse in der Entfernung $x$ vom Boden des Fasses; sie lässt sich durch Bestimmung des Umfanges leicht ausrechnen. Ist $h$ die Höhe des Fasses, so ist das Volumen gleich

V=\int _{0}^{h}q(x)\,\mathrm {d} x.

Die Keplersche Fassregel gibt nun

V={\frac {h}{6}}\cdot (q(0)+4q(h/2)+q(h))

als Näherungswert für das Volumen eines Fasses, dessen Querschnitt an drei Stellen bekannt ist.

Die Formel gibt das richtige Volumen für:

Kegel

$q(0)=0;q({\frac {h}{2}})={\frac {1}{4}}\cdot q(h);q(h)=R^{2}\pi$

$V_{Kegel}={\frac {h}{6}}\cdot (0+{\frac {4}{4}}\pi R^{2}+\pi R^{2})={\frac {h}{6}}\cdot (2\pi R^{2})={\frac {1}{3}}\cdot \pi R^{2}h$

Kegelstumpf

$q(0)=r^{2}\pi ;q({\frac {h}{2}})=({\frac {r+R}{2}})^{2}\cdot \pi ;q(h)=R^{2}\pi$ $V_{Kegelstumpf}={\frac {h}{6}}\cdot [r^{2}\pi +4\pi ({\frac {r+R}{2}})^{2}+\pi R^{2}]={\frac {h}{6}}\cdot [\pi r^{2}+{\frac {4}{4}}\pi \cdot (r^{2}+2rR+R^{2})+R^{2}]$ $={\frac {h}{6}}\pi \cdot [r^{2}+r^{2}+2rR+R^{2}+R^{2}]$ $={\frac {h}{6}}\pi \cdot [2r^{2}+2rR+2R^{2}]$ Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „http://localhost:6011/de.wikipedia.org/v1/“:): {\displaystyle =\frac {h}{3}\pi\cdot [r^2 + rR + R^2] }

Kugel

$q(0)=0;q({\frac {h}{2}})=R^{2}\pi ;q(h)=0;h=2R$

$V_{Kugel}={\frac {2R}{6}}\cdot (0+4\cdot \pi R^{2}+0)={\frac {2R}{6}}\cdot (4\pi R^{2})={\frac {4}{3}}\cdot \pi R^{3}$

Zylinder

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „http://localhost:6011/de.wikipedia.org/v1/“:): {\displaystyle q(0)=R^2 \pi; q(\frac{h}{2})= R^2 \pi ; q(h)= R^2 \pi }

$V_{Zylinder}={\frac {h}{6}}\cdot (\pi R^{2}+4\cdot \pi R^{2}+\pi R^{2})={\frac {h}{6}}\cdot (6\pi R^{2})={\frac {6h}{6}}\cdot \pi R^{2}=\pi R^{2}h$

Rotationsparaboloid

$q(0)=0;q({\frac {h}{2}})={\frac {1}{2}}R^{2}\pi ;q(h)=R^{2}\pi$

$V_{Paraboloid}={\frac {h}{6}}\cdot (0+{\frac {4}{2}}\cdot \pi R^{2}+\pi R^{2})={\frac {h}{6}}\cdot (3\pi R^{2})={\frac {h}{6}}\cdot 3\pi R^{2}={\frac {1}{2}}\pi R^{2}h$

Fass

Mathem. Definition:

Ein Rotationskörper, gebildet aus einer Mantelfläche, deren Erzeugende ein Kreisbogen ist, dessen Endpunkte den gleichen Abstand von der Rotationsachse haben, und zwei kongruenten Kreisflächen. Dazu gehört z.B. auch die symmetrische Kugelzone.

$q(0)=r^{2}\pi ;q({\frac {h}{2}})=R^{2}\pi ;q(h)=r^{2}\pi$

$V_{Fass}={\frac {h}{6}}\cdot (r^{2}\pi +4\cdot \pi R^{2}+\pi r^{2})={\frac {h}{6}}\cdot (2\pi r^{2}+4R^{2}\pi )$

Ist $u$ der Umfang von Boden und Deckel und $U$ der Umfang in der Mitte des Fasses, so ergibt sich daraus die Näherungsformel:

${\frac {h}{6}}\cdot [2\pi ({\frac {u}{2\pi }})^{2}+4({\frac {U}{2\pi }})^{2}\pi ]$ $={\frac {h}{6}}\cdot [2\pi {\frac {u^{2}}{4\pi ^{2}}}+4{\frac {U^{2}}{4\pi ^{2}}}\pi ]$

Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „http://localhost:6011/de.wikipedia.org/v1/“:): {\displaystyle =\frac h{12\pi}[u^2 + 2U^2].}

Siehe auch: Simpsonsche Formel, Newton-Cotes-Formeln

Land Sachsen

Keplersche Fassregel

What are your Feelings

Wissen

Automated Chatbot

Data Security

Virtual Reality

Communication

Support

Über uns

Impressum

Datenschutz

Company

About Us

Services

Features

Our Pricing

Latest News

Keplersche Fassregel

What are your Feelings

Share This Article :

Wissen

Automated Chatbot

Data Security

Virtual Reality

Communication

Support

Über uns

Impressum

Datenschutz

Company

About Us

Services

Features

Our Pricing

Latest News