Intervallarithmetik

Intervallarithmetik bezeichnet in der Mathematik eine Methodik zur automatisierten Fehlerabschätzung auf Basis abgeschlossener Intervalle. Vereinfacht gesagt, rechnet man nicht mehr mit Zahlen, sondern mit Intervallen, die nicht genau bekannte Werte repräsentieren. Hierfür werden einfache Rechenoperationen, wie die Grundrechenarten oder trigonometrische Funktionen, für das Rechnen mit Intervallen neu definiert, um äußere Grenzen eines gesuchten Wertebereiches zu erhalten. Ähnlich wie ein Fehlerbalken um einen Messwert, drückt ein Intervall das Ausmass der Unsicherheit bezüglich der zu berechnenden Größe aus.

Dieses Konzept eignet sich unter anderem zur Behandlung von Rundungsfehlern während der Berechnung und Unsicherheiten in der Kenntnis der exakten Werte physikalischer und technischer Parameter. Letztere ergeben sich oft aus Messfehlern und Bauteil-Toleranzen. Außerdem kann Intervallarithmetik dabei helfen, verlässliche Lösungen von Gleichungen und Optimierungsproblemen zu erhalten.

Einführung

Das Hauptaugenmerk bei der Intervallarithmetik liegt darauf, auf möglichst einfache Art und Weise obere und untere Schranken für den Wertebereich einer Funktion in einer oder mehreren Variablen zu bestimmen. Dabei müssen diese Schranken nicht unbedingt dem Supremum bzw. Infimum entsprechen, da die genaue Berechnung dieser Werte oft zu schwierig ist. (Es lässt sich zeigen, dass diese Aufgabenstellung im allgemeinen NP-schwer ist.)

Üblicherweise beschränkt man sich auf die Behandlung abgeschlossener, reeller Intervalle, also Mengen der Form

[a,b]=\{x\in \mathbb {R} \,|\,a\leq x\leq b\}

,

wobei auch $a={-\infty }$ und $b={\infty }$ zulässig sind. Dabei entsprechen $[{-\infty },b]$ und $[a,{\infty }]$ den meist halboffen geschriebenen Intervallen, die alle reellen Zahlen kleiner oder gleich $b$ bzw. größer oder gleich $a$ umfassen. Entsprechend bezeichnet das Intervall $[{-\infty },{\infty }]$ die gesamte reelle Achse.

Wie beim klassischen Rechnen mit Zahlen, muss zunächst einmal definiert werden, wie die arithmetischen Operationen und elementaren Funktionen auf Intervalle anzuwenden sind. Komplexere Funktionen können dann aus diesen Grundelementen zusammengesetzt werden Vorlage:Lit.

Grundrechenarten

Eine Operation $\star$ zwischen zwei Intervallen muss die Bedingung

[x_{1},x_{2}]\star [y_{1},y_{2}]=\{z\,|\,\exists x\in [x_{1},x_{2}]\wedge \exists y\in [y_{1},y_{2}]:z=x\star y\}

erfüllen. Für die vier Grundrechenarten folgt daraus, dass

[x_{1},x_{2}]\,\star \,[y_{1},y_{2}]=[\min(x_{1}\star y_{1},x_{1}\star y_{2},x_{2}\star y_{1},x_{2}\star y_{2}),\max(x_{1}\star y_{1},x_{1}\star y_{2},x_{2}\star y_{1},x_{2}\star y_{2})]

,

falls $x\star y$ zulässig ist für alle $x\in [x_{1},x_{2}]$ und $y\in [y_{1},y_{2}]$ .

Für praktische Anwendungen lässt sich dies noch weiter vereinfachen:

Addition: $[x_{1},x_{2}]+[y_{1},y_{2}]=[x_{1}+y_{1},x_{2}+y_{2}]$
Subtraktion: $[x_{1},x_{2}]-[y_{1},y_{2}]=[x_{1}-y_{2},x_{2}-y_{1}]$
Multiplikation: $[x_{1},x_{2}]\cdot [y_{1},y_{2}]=[\min(x_{1}y_{1},x_{1}y_{2},x_{2}y_{1},x_{2}y_{2}),\max(x_{1}y_{1},x_{1}y_{2},x_{2}y_{1},x_{2}y_{2})]$
Division: $[x_{1},x_{2}]/[y_{1},y_{2}]=[x_{1},x_{2}]\cdot (1/[y_{1},y_{2}])$ , wobei $1/[y_{1},y_{2}]=[1/y_{2},1/y_{1}]$ falls $0\notin [y_{1},y_{2}]$ .

Für die Division durch ein Intervall, das die Null enthält, definiert man zunächst einmal

1/[y_{1},0]=[-\infty ,1/y_{1}]

und

1/[0,y_{2}]=[1/y_{2},\infty ]

.

Für $y_{1}<0<y2$ gilt $1/[y_{1},y_{2}]=[-\infty ,1/y_{1}]\cup [1/y_{2},\infty ]$ , so dass man eigentlich $1/[y_{1},y_{2}]=[-\infty ,\infty ]$ setzten müsste. Dadurch verliert man allerdings die Lücke $(1/y_{1},1/y_{2})$ und damit wertvolle Informationen. Üblicherweise rechnet man daher mit den Teilmengen $[-\infty ,1/y_{1}]$ und $[1/y_{2},\infty ]$ einzeln weiter.

Weil innerhalb einer Intervallrechnung auch mehrere solcher Aufspaltungen auftreten können, ist es manchmal sinnvoll das Rechnen mit sogenannten Multi-Intervallen der Form $\textstyle \bigcup _{i=1}^{l}[x_{i1},x_{i2}]$ zu systematisieren. Die entsprechende Multi-Intervall-Arithmetik pflegt dann eine disjunkte Menge von Intervallen und sorgt dann beispielsweise auch dafür, sich überschneidende Intervalle zu vereinigen Vorlage:Lit.

Da man eine Zahl $r\in \mathbb {R}$ als das Intervall $[r,r]$ interpretieren kann, erhält man sofort eine Vorschrift zur Kombination von intervall- und reellwertigen Größen.

Mit Hilfe dieser Definitionen lässt sich bereits der Wertebereich einfacher Funktionen, wie $f(a,b,x)=a\cdot x+b$ bestimmen. Setzt man beispielsweise $a=[1,2]$ , $b=[5,7]$ und $x=[2,3]$ , so ergibt sich

f(a,b,x)=([1,2]\cdot [2,3])+[5,7]=[1\cdot 2,2\cdot 3]+[5,7]=[7,13]

.

Interpretiert man $f(a,b,x)$ als Funktion einer Variablen $x$ mit intervallwertigen Parametern $a$ und $b$ , dann lässt sich die Menge aller Nullstellen dieser Funktionenschar leicht bestimmen. Es gilt dann

f([1,2],[5,7],x)=([1,2]\cdot x)+[5,7]=0\Leftrightarrow [1,2]\cdot x=[-7,-5]\Leftrightarrow x=[-7,-5]/[1,2]

,

die möglichen Nullstellen liegen also im Intervall $[-7,{-2.5}]$ .

Wie im obigen Beispiel, kann die Multiplikation von Intervallen oft auf die Multiplikation nur zweier Zahlen zurückgeführt werden. Es gilt nämlich

[x_{1},x_{2}]\cdot [y_{1},y_{2}]=[x_{1}\cdot y_{1},x_{2}\cdot y_{2}]

, falls

x_{1},y_{1}\geq 0

.

Die Multiplikation lässt sich hier als Flächenbestimmung eines Rechtecks mit variierenden Kantenlängen interpretieren. Das intervallwertige Ergebnis deckt dann alle Werte von der kleinst- bis zu größtmöglichen Fläche ab.

Entsprechendes gilt, wenn eines der beiden Intervalle ganz im nicht-positiven und das andere ganz im nicht-negativen Bereich der reellen Achse liegt. Generell muss bei der Multiplikation noch beachtet werden, dass das Ergebnis sofort auf $[{-\infty },{\infty }]$ gesetzt werden muss, falls unbestimmte Werte, wie $0\cdot \infty$ auftreten. Dies tritt z. B. bei einer Division auf, bei der Zähler und Nenner beide Null enthalten.

Notation

Um intervallwertige Größen leichter in Formeln zu erkennen, zweckentfremdet man die eckigen Klammern zur „Markierung“.

Dementsprechend bezeichnet $[x]\equiv [x_{1},x_{2}]$ ein Intervall und die Menge aller reellen Intervalle wird als

[\mathbb {R} ]:=\{\,[x_{1},x_{2}]\,|\,x_{1}\leq x_{2}\wedge x_{1},x_{2}\in \mathbb {R} \cup \{-\infty ,\infty \}\}

abgekürzt. Für eine Box oder einen Vektor von Intervallen $([x]_{1},\cdots ,[x]_{n})\in [\mathbb {R} ]^{n}$ verwendet man zusätzlich fetten Schriftschnitt: $[\mathbf {x} ]$ .

Bei einer derart kompakten Notation ist zu beachten, dass $[x]$ nicht mit einem sogenannten uneigentlichen Intervall $[x_{1},x_{1}]$ verwechselt wird, bei dem obere und untere Grenze übereinstimmen.

Elementare Funktionen

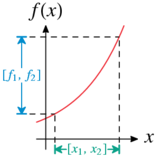
Da man auch Funktionen mit Intervallmethoden behandeln möchte, die Terme enthalten, die sich nicht aus den Grundrechenarten ergeben, muss man auch noch weitere elementare Funktionen für Intervalle neu definieren. Dabei nutzt man vorhandene Monotonieeigenschaften aus.

Für monotone Funktionen in einer Variablen lässt sich der Wertebereich ebenfalls leicht bestimmen. Ist $f:\mathbb {R} \rightarrow \mathbb {R}$ monoton steigend oder fallend in einem Intervall $[x_{1},x_{2}]$ , dann gilt für alle Werte $y_{1},y_{2}\in [x_{1},x_{2}]$ mit $y_{1}\leq y_{2}$ die Ungleichung

f(y_{1})\leq f(y_{2})

, bzw.

f(y_{1})\geq f(y_{2})

.

Den Wertebereich des Intervalls $[y_{1},y_{2}]\subseteq [x_{1},x_{2}]$ erhält man durch Auswerten der Funktion an den Endpunkten $y_{1}$ und $y_{2}$ :

f([y_{1},y_{2}])=[\min(f(y_{1}),f(y_{2})),\max(f(y_{1}),f(y_{2}))]

.

Daher lassen sich folgende Intervallisierungen elementarer Funktionen leicht definieren:

Exponentialfunktion: $e^{[x_{1},x_{2}]}=[e^{x_{1}},e^{x_{2}}]$ ,
Logarithmus: $\log({[x_{1},x_{2}]})=[\log {x_{1}},\log {x_{2}}]$ , bzw. $\ln({[x_{1},x_{2}]})=[\ln {x_{1}},\ln {x_{2}}]$ , für positive Intervalle $[x_{1},x_{2}]$
Ungerade Potenzen: ${[x_{1},x_{2}]}^{n}=[{x_{1}}^{n},{x_{2}}^{n}]$ , für ungerade $n\in \mathbb {N}$ .

Es ist außerdem noch wichtig, den Wertebereich für gerade Potenzen bestimmen zu können. Im Gegensatz zur üblichen Numerik, ist es hier nicht sinnvoll, die Berechnung auf die Multiplikation zurückzuführen. Beispielsweise bewegt sich $x^{n}$ für $x\in [-1,1]$ innerhalb des Intervalles $[0,1]$ , wenn $n=2,4,6,\ldots$ . Versucht man $[-1,1]^{n}$ aber durch Multiplikationen der Form $[-1,1]\cdot \ldots \cdot [-1,1]$ zu bestimmen, so erhält man in jedem Fall als Ergebnis $[-1,1]$ .

Sinnvoller ist es hier, die Parabel $x^{n}$ als Zusammensetzung einer monoton fallenden (für $x<0$ ) und einer monoton steigenden Funktion (für $x>0$ ) zu betrachten. Es gilt also für gerade $n\in \mathbb {N}$ :

${[x_{1},x_{2}]}^{n}=[x_{1}^{n},x_{2}^{n}]$ , falls $x_{1}\leq 0$ ,
${[x_{1},x_{2}]}^{n}=[x_{2}^{n},x_{1}^{n}]$ , falls $x_{2}<0$ ,
${[x_{1},x_{2}]}^{n}=[0,\max(x_{1}^{n},x_{2}^{n})]$ , sonst.

Allgemeiner kann man sagen, dass es für stückweise monotone Funktionen ausreicht, diese an den Endpunkten $x_{1},x_{2}$ eines Intervalls $[x_{1},x_{2}]$ , sowie an den in $[x_{1},x_{2}]$ enthaltenen sogenannten kritischen Punkten auszurechnen. Die kritischen Punkte entsprechen hierbei den Stellen, an denen sich die Monotonieeigenschaften ändern.

Dies lässt sich z. B. auf Sinus und Kosinus anwenden, die zusätzlich an Stellen $({1}/{2}+{n})\,\pi$ bzw. ${n}\,\pi$ für alle $n\in \mathbb {Z}$ ausgewertet werden müssen. Hierbei spielen höchstens fünf Punkte eine Rolle, da man als Ergebnis sofort $[-1,1]$ festlegen kann, wenn das Eingangsintervall mindestens eine ganze Periode enthält. Außerdem müssen Sinus und Kosinus lediglich an den Randpunken neu evaluiert werden, da die entsprechenden Werte an den kritischen Stellen – nämlich -1, 0 , +1 – vorab abgespeichert werden können.

Intervallerweiterungen allgemeiner Funktionen

Im Allgemeinen findet man für beliebige Funktionen keine derart einfache Beschreibung des Wertebereiches. Man kann diese aber oft auf Intervalle ausdehnen. Wenn $f:\mathbb {R} ^{n}\rightarrow \mathbb {R}$ eine Funktion ist, die einen reellwertigen Vektor auf eine reelle Zahl abbildet, dann nennt man $[f]:[\mathbb {R} ]^{n}\rightarrow [\mathbb {R} ]$ eine Intervallerweiterung von $f$ , wenn gilt

[f]([\mathbf {x} ])\supseteq \{f(\mathbf {y} )|\mathbf {y} \in [\mathbf {x} ]\}

.

Dies definiert die Intervallerweiterung nicht eindeutig. So sind beispielsweise sowohl $[f]([x_{1},x_{2}])=[e^{x_{1}},e^{x_{2}}]$ als auch $[g]([x_{1},x_{2}])=[{-\infty },{\infty }]$ zulässige Erweiterungen der Exponentialfunktion. Da möglichst scharfe Erweiterungen gewünscht sind, also solche, die so genau wie möglich den gesuchten Wertebereich approximieren, wird man in diesem Fall eher $[f]$ wählen, da sie sogar den exakten Bereich bestimmt.

Die natürliche Intervallerweiterung erhält man, indem man in der Funktionsvorschrift $f(x_{1},\cdots ,x_{n})$ die Grundrechenarten und elementaren Funktionen durch ihre intervallwertigen Äquivalente ersetzt.

Die Taylor-Intervallerweiterung (vom Grad $k$ ) einer $k+1$ mal differenzierbaren Funktion $f$ ist definiert durch

[f]([\mathbf {x} ]):=

f(\mathbf {y} )+\sum _{i=1}^{k}{\frac {1}{i!}}\mathrm {D} ^{i}f(\mathbf {y} )\cdot ([\mathbf {x} ]-\mathbf {y} )^{i}+[r]([\mathbf {x} ],[\mathbf {x} ],\mathbf {y} )

,

für ein $\mathbf {y} \in [\mathbf {x} ]$ ,

wobei $\mathrm {D} ^{i}f(\mathbf {y} )$ das Differential $i$ -ter Ordnung von $f$ am Punkt $\mathbf {y}$ und $[r]$ eine Intervallerweiterung des Taylorrestgliedes

r(\mathbf {x} ,\xi ,\mathbf {y} )={\frac {1}{(k+1)!}}\mathrm {D} ^{k+1}f(\xi )\cdot (\mathbf {x} -\mathbf {y} )^{k+1}

bezeichnet.

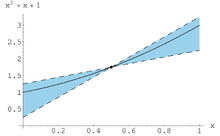
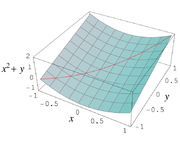
Da der Vektor $\xi$ zwischen $\mathbf {x}$ und $\mathbf {y}$ mit $\mathbf {x} ,\mathbf {y} \in [\mathbf {x} ]$ liegt, lässt sich $\xi$ ebenfalls durch $[\mathbf {x} ]$ abschätzen. Üblicherweise wählt man für $\mathbf {y}$ den Mittelpunkt des Intervallvektors und die natürliche Intervallerweiterung zur Abschätzung des Restgliedes.

Den Spezialfall der Taylor-Intervallerweiterung vom Grad $k=0$ bezeichnet man auch als Mittelwert-Intervallerweiterung. Für eine Intervallerweiterung der Jacobi-Matrix $[J_{f}](\mathbf {[x]} )$ erhält man hier

[f]([\mathbf {x} ]):=f(\mathbf {y} )+[J_{f}](\mathbf {[x]} )\cdot ([\mathbf {x} ]-\mathbf {y} )

.

Eine nichtlineare Funktion kann so durch lineare Funktionen eingegrenzt werden.

Intervallverfahren

Die Methoden der klassischen Numerik können nicht direkt für die Intervallarithmetik umgesetzt werden, da hierbei Abhängigkeiten meist nicht berücksichtigt werden.

Gerundete Intervallarithmetik

Um effizient mit Intervallen rechnen zu können, muss eine konkrete Implementierung kompatibel zum Rechnen mit Gleitkommazahlen sein. Die oben definierten Operationen basieren auf exakter Arithmetik, die bei schnellen numerischen Lösungsverfahren nicht zur Verfügung steht. Der Wertebereich der Funktion $f(x,y)=x+y$ für $x\in [0.1,0.8]$ und $y\in [0.06,0.08]$ wäre beispielsweise $[0.16,0.88]$ . Führt man die gleiche Rechnung mit einstelliger Präzision durch, so würde das Ergebnis üblicherweise zu $[0.2,0.9]$ gerundet. Da aber $[0.2,0.9]\not \supseteq [0.16,0.88]$ würde dieser Ansatz den Grundprinzipien der Intervallarithmetik widersprechen, da ein Teil des Wertebereiches von $f([0.1,0.8],[0.06,0.08])$ verloren geht. Stattdessen ist hier die nach außen gerundete Lösung $[0.1,0.9]$ vorzuziehen.

Die Norm IEEE 754 definiert neben Standarddarstellungen binärer Gleitkommazahlen auch genaue Verfahren für die Durchführung von Rundungen. Demnach muss ein zu IEEE 754 konformes System dem Programmierer neben dem mathematischen Runden (zur nächsten Gleitkommazahl) noch weitere Rundungsmodi bereitstellen: immer aufrunden, immer abrunden und Rundung gegen 0 (Ergebnis betragsmäßig verkleinern).

Das benötigte nach außen Runden lässt sich also durch entsprechendes Umschalten der Rundungseinstellungen der CPU beim Berechnen von oberer und unterer Grenze bewerkstelligen. Alternativ kann dies durch Hinzuaddition eines geeigneten schmalen Intervalls $[\varepsilon _{1},\varepsilon _{2}]$ erreicht werden.

Abhängigkeitsproblem und Einhüllungseffekt

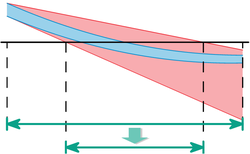
Das sogenannte Abhängigkeitsproblem ist ein Haupthindernis bei der Anwendung der Intervallarithmetik. Obwohl der Wertebereich der elementaren arithmetischen Operationen und Funktionen mit Intervallmethoden sehr genau bestimmt werden kann, gilt dies nicht mehr für zusammengesetzte Funktionen. Falls ein intervallwertiger Parameter mehrfach in einer Rechnung auftritt, wird jedes Auftreten unabhängig voneinander behandelt. Dies führt zu einer ungewollten Aufblähung der resultierenden Intervalle.

Zur Illustration sei eine Funktion $f$ durch den Ausdruck $f(x)=x^{2}+x$ gegeben. Der Wertebereich dieser Funktion über dem Intervall $[-1,1]$ beträgt eigentlich $[-1/4,2]$ . Um die natürliche Intervallerweiterung zu erhalten, rechnet man aber $[-1,1]^{2}+[-1,1]=[0,1]+[-1,1]=[-1,2]$ , was einen etwas größeren Bereich ergibt. In der Tat berechnet man eigentlich Infimum und Supremum der Funktion $h(x,y)=x^{2}+y$ über $x,y\in [-1,1]$ . Hier würde man also besser eine alternative Formulierung für $f$ verwenden, die die Variable $x$ nur einmal verwendet. In diesem Fall kann man den Ausdruck $f(x)=x^{2}+x$ einfach durch quadratische Ergänzung zu $f(x)=\left(x+{\frac {1}{2}}\right)^{2}-{\frac {1}{4}}$ umformen.

Dann liefert die entsprechende Intervallrechnung

\left([-1,1]+{\frac {1}{2}}\right)^{2}-{\frac {1}{4}}=\left[-{\frac {1}{2}},{\frac {3}{2}}\right]^{2}-{\frac {1}{4}}=\left[0,{\frac {9}{4}}\right]-{\frac {1}{4}}=\left[-{\frac {1}{4}},2\right]

auch den richtigen Wertebereich.

Im Allgemeinen lässt sich zeigen, dass man tatsächlich den genauen Wertebereich erhält, wenn jede Variable nur einmal auftaucht. Allerdings lässt sich nicht jede Funktion geeignet auflösen.

Die durch das Abhängigkeitsproblem verursachte Überschätzung des Wertebereiches, kann soweit gehen, dass das Resultat einen derart großen Bereich umfasst, der keine sinnvollen Schlüsse mehr zulässt.

Eine zusätzliche Vergrößerung des Wertebereichs ergibt sich aus dem Einhüllen von Bereichen, die nicht die Form eines Intervallvektors haben. Die Lösungsmenge des linearen Systems

{\begin{matrix}x&=&y\\x&=&p\end{matrix}}

für

p\in [-1,1]

ist genau die Gerade zwischen den Punkte $(-1,-1)$ und $(1,1)$ . Intervallmethoden liefern hier aber im besten Fall das Quadrat $[-1,1]\times [-1,1]$ , das die tatsächliche Lösung einhüllt (Einhüllungs- oder „Wrapping“-Effekt).

Lineare Intervallsysteme

Ein lineares Intervallsystem besteht aus einer intervallwertigen Matrix $[\mathbf {A} ]\in [\mathbb {R} ]^{n\times m}$ und einem Intervallvektor $[\mathbf {b} ]\in [\mathbb {R} ]^{n}$ . Gesucht ist dann eine möglichst schmale Box $[\mathbf {x} ]\in [\mathbb {R} ]^{m}$ , die alle Vektoren $\mathbf {x} \in \mathbb {R} ^{m}$ enthält, für die es ein Paar $(\mathbf {A} ,\mathbf {b} )$ mit $\mathbf {A} \in [\mathbf {A} ]$ und $\mathbf {b} \in [\mathbf {b} ]$ gibt, das die Gleichung

\mathbf {A} \cdot \mathbf {x} =\mathbf {b}

erfüllt.

Für quadratische Systeme - also für $n=m$ - lässt sich ein solcher Intervallvektor $[\mathbf {x} ]$ , der alle möglichen Lösungen enthält, sehr einfach mit dem Intervall-Gauß Verfahren bestimmen. Hierfür ersetzt man die numerischen Operationen, die bei dem aus der linearen Algebra bekannten gaußschen Eliminationsverfahren auftauchen, durch ihre Intervallversionen. Da allerdings während der Abarbeitung dieser Methode die intervallwertigen Einträge von $[\mathbf {A} ]$ und $[\mathbf {b} ]$ mehrfach in die Rechnung eingehen, leidet dieser Ansatz sehr stark an dem Abhängigkeitsproblem. Folglich bietet sich der Intervall-Gauß nur für grobe erste Abschätzungen an, die zwar die gesamte Lösungsmenge enthalten, aber auch einen sehr großen Bereich außerhalb davon.

Eine grobe Lösung $[\mathbf {x} ]$ kann oft durch eine Intervallisierung des Gauß-Seidel-Verfahrens verbessert werden. Diese ist folgendermaßen motiviert: Die $i$ -te Zeile der intervallwertigen linearen Gleichung

{\begin{pmatrix}{[a_{11}]}&\cdots &{[a_{1n}]}\\\vdots &\ddots &\vdots \\{[a_{n1}]}&\cdots &{[a_{nn}]}\end{pmatrix}}\cdot {\begin{pmatrix}{x_{1}}\\\vdots \\{x_{n}}\end{pmatrix}}={\begin{pmatrix}{[b_{1}]}\\\vdots \\{[b_{n}]}\end{pmatrix}}

lässt sich nach der Variablen $x_{i}$ auflösen, falls die Division $1/[a_{ii}]$ erlaubt ist. Es gilt demnach gleichzeitig

x_{j}\in [x_{j}]

und

x_{j}\in ([b_{i}]-\sum _{k\not =j}[a_{ik}]\cdot [x_{k}])/[a_{ij}]

.

Man kann also nun $[x_{j}]$ durch

[x_{j}]\cap ([b_{i}]-\sum _{k\not =j}[a_{ik}]\cdot [x_{k}])/[a_{ij}]

ersetzen, und so den Vektor $[\mathbf {x} ]$ elementweise verbessern. Da das Verfahren effizienter für diagonaldominante Matrizen ist, versucht man oft statt dem System $[\mathbf {A} ]\cdot \mathbf {x} =[\mathbf {b} ]{\mbox{,}}$ die durch Multiplikation mit einer geeigneten reellen Matrix $\mathbf {M}$ entstandene Matrixgleichung

(\mathbf {M} \cdot [\mathbf {A} ])\cdot \mathbf {x} =\mathbf {M} \cdot [\mathbf {b} ]

zu lösen. Wählt man beispielsweise $\mathbf {M} =\mathbf {A} ^{-1}$ für die Mittelpunktsmatrix $\mathbf {A} \in [\mathbf {A} ]$ , so ist $\mathbf {M} \cdot [\mathbf {A} ]$ eine äußere Näherung der Einheitsmatrix.

Für die oben genannten Methoden gilt allerdings, dass sie nur dann gut funktionieren, wenn die Breite der vorkommenden Intervalle hinreichend klein ist. Für breitere Intervalle kann es sinnvoll sein, ein Intervall-lineares System auf eine endliche (wenn auch große) Anzahl reellwertiger linearer Systeme zurückzuführen. Sind nämlich alle Matrizen $\mathbf {A} \in [\mathbf {A} ]$ invertierbar, so ist es vollkommen ausreichend alle möglichen Kombinationen an (oberen und unteren) Endpunkten der vorkommenden Intervalle zu betrachten. Die resultierenden Teilprobleme können dann mit herkömmlichen numerischen Methoden gelöst werden. Intervallarithmetik wird lediglich noch benutzt, um Rundungsfehler zu bestimmen

Dieser Ansatz ist allerdings nur für Systeme kleinerer Dimension möglich, da bei einer vollbesetzten $n\times n$ Matrix schon $2^{n^{2}}$ reelle Matrizen invertiert werden müssen, mit jeweils $2^{n}$ Vektoren für die rechte Seite. Dieser Ansatz wurde von Jiří Rohn noch weitergeführt und verbessert ^[1].

Intervall-Newton Verfahren

Eine Intervallvariante des Newton-Verfahrens zur Bestimmung der Nullstellen in einem Intervallvektor $[\mathbf {x} ]$ lässt sich einfach aus der Mittelwert-Erweiterung ableiten Vorlage:Lit. Für einen unbekannten Vektor $\mathbf {z} \in [\mathbf {x} ]$ gilt für ein festes $\mathbf {y} \in [\mathbf {x} ]$ , dass

f(\mathbf {z} )\in f(\mathbf {y} )+[J_{f}](\mathbf {[x]} )\cdot (\mathbf {z} -\mathbf {y} )

.

Für eine Nullstelle $\mathbf {z}$ ist $f(z)=0$ , und somit muss

f(\mathbf {y} )+[J_{f}](\mathbf {[x]} )\cdot (\mathbf {z} -\mathbf {y} )=0

.

erfüllt sein. Man erhält also $\mathbf {z} \in \mathbf {y} -[J_{f}](\mathbf {[x]} )^{-1}\cdot f(\mathbf {y} )$ . Eine äußere Abschätzung von $[J_{f}](\mathbf {[x]} )^{-1}\cdot f(\mathbf {y} ))$ kann hierbei durch eines der linearen Verfahren bestimmt werden.

In jedem Newton-Schritt wird nun ein grober Startwert $[\mathbf {x} ]\in [\mathbb {R} ]^{n}$ durch $[\mathbf {x} ]\cap \left(\mathbf {y} -[J_{f}](\mathbf {[x]} )^{-1}\cdot f(\mathbf {y} )\right)$ ersetzt und so iterativ verbessert. Im Gegensatz zum klassischen Verfahren nähert sich diese Methode von außen den Nullstellen. Daher ist garantiert, dass das Ergebnis immer alle Nullstellen im Startwert enthält. Umgekehrt hat man bewiesen, dass $f$ keine Nullstelle in $[\mathbf {x} ]$ hat, wenn der Newton-Schritt die leere Menge zurückliefert.

Das Verfahren konvergiert gegen eine Menge, die alle Nullstellen (innerhalb der Startregion) enthält. Durch in diesem Fall vorhandene Divisionen durch Null entstehen oft mehrere Intervallvektoren, die die Nullstellen voneinander trennen. Diese Trennung ist nicht immer vollständig, und kann dann durch Bisektion forciert werden.

Als Beispiel betrachte man die Funktion $f(x)=x^{2}-2$ , den Startwert $[x]=[-2,2]$ und den Punkt $y=0$ . Man hat dann $J_{f}(x)=2\,x$ und der erste Newton-Schritt ist gegeben durch

[-2,2]\cap \left(0-{\frac {1}{2\cdot [-2,2]}}(0-2)\right)=[-2,2]\cap \left([{-\infty },{-0.5}]\cup [{0.5},{\infty }]\right)

.

Es gilt also für eine Nullstelle $x\in [{-2},{-0.5}]\cup [{0.5},{2}]$ . Weitere Newtonschritte werden dann jeweils auf $x\in [{-2},{-0.5}]$ und $[{0.5},{2}]$ getrennt angewendet. Diese konvergieren zu beliebig kleinen Intervallen um $-{\sqrt {2}}$ und $+{\sqrt {2}}$ .

Das Intervall-Newton-Verfahren lässt sich auch ohne weiteres bei dicken Funktionen anwenden, also Funktionen wie $g(x)=x^{2}-[2,3]$ , die bereits dann Intervalle zurückliefern, wenn man reelle Zahlen einsetzt. Die Lösung besteht dann aus mehreren Intervallen $[-{\sqrt {3}},-{\sqrt {2}}]\cup [{\sqrt {2}},{\sqrt {3}}]$ .

Bisektion und Überdeckungen

Die verschiedenen Intervallmethoden liefern nur äußerst konservative Abschätzungen eines jeweils gesuchten Bereiches, da Abhängigkeiten zwischen den intervallwertigen Größen nicht ausreichend berücksichtigt werden. Das Abhängigkeitsproblem spielt aber eine desto geringere Rolle, je dünner die Intervalle sind.

Überdeckt man einen Intervallvektor $[\mathbf {x} ]$ durch kleinere Boxen $[\mathbf {x} _{1}],\cdots ,[\mathbf {x} _{k}]{\mbox{,}}$ so dass $\textstyle [\mathbf {x} ]=\bigcup _{i=1}^{k}[\mathbf {x} _{i}]{\mbox{,}}$ dann gilt für den Wertebereich $\textstyle f([\mathbf {x} ])=\bigcup _{i=1}^{k}f([\mathbf {x} _{i}]){\mbox{.}}$ Für die oben genannten Intervallerweiterungen gilt dann $\textstyle [f]([\mathbf {x} ])\supseteq \bigcup _{i=1}^{k}[f]([\mathbf {x} _{i}])$ . Da $[f]([\mathbf {x} ])$ oft eine echte Obermenge der rechten Seite ist, erhält man somit meist eine verbesserte Abschätzung.

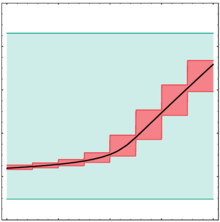
Eine solche Überdeckung kann zum einen durch Bisektion generiert werden, indem man besonders dicke Elemente $[x_{i1},x_{i2}]$ des Intervallvektors $[\mathbf {x} ]=([x_{11},x_{12}],\cdots ,[x_{n1},x_{n2}])$ beispielsweise in der Mitte teilt und durch zwei Intervalle $[x_{i1},(x_{i1}+x_{i2})/2]$ und $[(x_{i1}+x_{i2})/2,x_{i2}]$ ersetzt. Sollte das daraus folgende Resultat immer noch nicht geeignet sein, kann sukzessive weiter zerlegt werden. Hierbei gilt allerdings zu beachten, dass durch $r$ geteilte Vektorelemente eine Überdeckung aus $2^{r}$ Intervallvektoren entsteht, was den Rechenaufwand natürlich stark erhöht.

Bei sehr breiten Intervallen kann es sogar sinnvoll sein, alle Intervalle gleich in mehrere Teilintervalle mit (kleiner) konstanter Breite zu zerlegen („Mincing“). Damit spart man die Zwischenrechnung für die einzelnen Bisektionsschritte. Beide Herangehensweisen sind allerdings nur für Probleme niedriger Dimension geeignet.

Anwendung

Die Intervallarithmetik kommt auf verschiedenen Gebieten zum Einsatz, um Größen zu behandeln, für die keine genauen Zahlenwerte festgelegt werden können Vorlage:Lit.

Rundungsfehleranalyse

Die Intervallarithmetik wird bei der Fehleranalyse angewendet, um Kontrolle über die bei jeder Berechnung auftretenden Rundungsfehler zu bekommen. Der Vorteil der Intervallarithmetik liegt darin, dass man nach jeder Operation ein Intervall erhält, welches das Ergebnis sicher einschließt. Aus dem Abstand der Intervallgrenzen kann man den aktuellen Berechnungsfehler direkt ablesen:

Fehler =

\mathrm {abs} (a-b)

für gegebenes Intervall

[a,b]

.

Intervallanalyse bietet hierbei keinen Ersatz für die klassischen Methoden zur Fehlerreduktion, wie Pivotisierung, sondern ergänzt diese lediglich.

Toleranzanalyse

Bei der Simulation technischer und physikalischer Prozesse treten oft Parameter auf, denen keine exakten Zahlenwerte zugeordnet werden können. So unterliegt der Produktionsprozess technischer Bauteile gewissen Toleranzen, so bestimmte Parameter innerhalb bestimmter Intervalle schwanken können. Außerdem können viele Naturkonstanten nicht mit beliebiger Genauigkeit gemessen werden Vorlage:Lit.

Wird das Verhalten eines solchen toleranzbehafteten Systems beispielsweise durch eine Gleichung $f(\mathbf {x} ,\mathbf {p} )=0$ , für $\mathbf {p} \in [\mathbf {p} ]$ und Unbekannten $\mathbf {x}$ , beschrieben, dann kann die Menge aller möglichen Lösungen

\{\mathbf {x} \,|\,\exists \mathbf {p} \in [\mathbf {p} ],f(\mathbf {x} ,\mathbf {p} )=0\}

,

durch Intervallmethoden abgeschätzt werden. Diese stellen hier eine Alternative zur klassischen Fehlerrechnung dar. Im Gegensatz zu punktbasierten Methoden, wie der Monte-Carlo-Simulation, stellt die verwendete Methodik sicher, dass keine Teile des Lösungsgebietes übersehen werden. Allerdings entspricht das Ergebnis immer einer Worst Case-Analyse für gleichverteilte Fehler, andere Wahrscheinlichkeitsverteilungen sind nicht möglich.

Fuzzy-Arithmetik

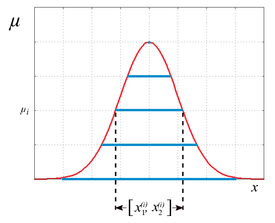
Intervallarithmetik kann auch dazu verwendet werden, Fuzzy-Logik auf allgemeine Wahrscheinlichkeitsverteilungen zu erweitern. Neben den Aussagen $x\in [x]$ und $x\not \in [x]$ werden auch endlich viele Zwischenwerte, die Zugehörigkeitsstufen $\mu _{i}\in [0,1]$ , betrachtet. Für die Fuzzy-Arithmetik^[2] wird die Form einer solchen Verteilung für einen unscharfen Wert durch eine Reihe von Intervallen

[x^{(1)}]\supset [x^{(2)}]\supset \cdots \supset [x^{(k)}]

angenähert. Dabei entspricht das Intervall $[x^{(i)}]$ dem Schwankungsbereich für die Stufe $\mu _{i}$ .

Die entsprechende Verteilung für eine Funktion $f(x_{1},\cdots ,x_{n})$ bezüglich unscharfer Werte $x_{1},\cdots ,x_{n}$ und den entsprechenden Sequenzen $x_{1}\in [x_{1}^{(1)}]\supset \cdots \supset [x_{1}^{(k)}],\cdots ,x_{n}\in [x_{n}^{(1)}]\supset \cdots \supset [x_{n}^{(k)}]$ lässt sich dann durch die Intervallsequenz $[y{(1)}]\supset \cdots \supset [y^{(k)}]$ approximieren. Die Werte $[y^{(i)}]$ sind gegeben durch $[y^{(i)}]=f([x_{1}^{(i)}],\cdots [x_{n}^{(i)}])$ und können durch Intervallverfahren abgeschätzt werden. Dabei entspricht $[y^{(1)}]$ dem Ergebnis einer Intervallrechnung, wohingegen $[y^{(k)}]$ mit der klassischen Numerik übereinstimmt.

Geschichtliches

Als Geburtsstunde der Intervallarithmetik wird das Erscheinen des Buches Interval Analysis von Ramon E. Moore im Jahr 1966 Vorlage:Lit angesehen. Die Idee dazu hatte er im Frühjahr 1958 und bereits ein knappes Jahr später veröffentlichte er einen Artikel über computerunterstützte Intervallarithmetik ^[3].

Unabhängig davon hatte Mieczyslaw Warmus zwar schon 1956 Formeln für das Rechnen mit Intervallen vorgeschlagen ^[4], bei Moore fanden sich aber neben Implementierungshinweisen auch erste nicht-triviale Anwendungen.

Implementierungen

Es gibt viele Softwarepakete, welche die Entwicklung numerischer Anwendungen unter Nutzung der Intervallarithmetik erlauben ^[5]. Diese sind meist in Form von Programmbibliotheken umgesetzt ^[6]. Es gibt allerdings auch C++- und Fortran-Übersetzer, welche Intervall Datentypen und entsprechend geeignete Operationen als Spracherweiterung ^[7] besitzen, so dass Intervallarithmetik direkt unterstützt wird.

Patente

William G. Walster (Sun Microsystems) hat – teilweise zusammen mit Ramon E. Moore und Eldon R. Hansen – mehrere Patente im Bereich der Intervallarithmetik beim U.S. Patent and Trademark Office angemeldet ^[8]. Die Gültigkeit dieser Ansprüche ist jedoch in der Intervallarithmetik-Forschungsgemeinde stark umstritten, da sie möglicherweise lediglich den bisherigen Stand der Technik wiedergeben.

Siehe auch

Referenzen

Literatur

Alexander Dreyer: Interval Analysis of Analog Circuits with Component Tolerances. Doktorarbeit, Shaker Verlag, Aachen, 2005, ISBN 3-8322-4555-3.
Eldon R. Hansen: Global optimization using interval methods. Band 165 von Monographs and textbooks in pure and applied mathematics. Marcel Dekker, New York, 1992, ISBN 0-8247-4059-9.
Jürgen Herzberger. Basic definitions and properties of interval arithmetic. In Jürgen Herzberger (Hrsg.), Topics in validated computations, Seiten 1-6. Elsevier Science B.V., Amsterdam, 1993, ISBN 0-12-049820-0.
L. Jaulin, M. Kieffer, O. Didrit, and É.Walter: Applied Interval Analysis: With examples in parameter estimation robust control and robotics. Springer, London, 2001, ISBN 1-85233-219-0.
Günter Mayer, Grundbegriffe der Intervallrechnung. In Ulrich Kulisch (Hrsg.): Wissenschaftliches Rechnen mit Ergebnisverifikation, S. 101-118, Akademie-Verlag, Berlin 1989; auch: Vieweg-Verlag, Wiesbaden 1989, ISBN 3-528-08943-1.
R. E. Moore: Interval Analysis. Prentice-Hall, Englewood Cliff, NJ, 1966, ISBN 0-13-476853-1.

Weblinks

Quellen

Dieser Artikel nimmt am Schreibwettbewerb teil. Bitte hilf mit, ihn zu verbessern!

[1] Veröffentlichugen von Jiří Rohn

[2] Fuzzy-Methoden, Zusammenstellung von Michael Hanss, Universität Stuttgart

[3] Abhandlung über frühe Artikel von R. E. Moore

[4] Frühe Arbeiten von M. Warmus

[5] Software für Intervallrechnungen, zusammengestellt von Vladik Kreinovich, University of Texas, El Paso

[6] Beispiel einer Intervallarithmetik-Klasse in C++ von Sun Microsystems

[7] C++- und Fortran-Compiler mit Intervallunterstützung von Sun Microsystems

[8] Patentschriften unter Anwendung von Intervallarithmetik beim U.S. Patent and Trademark Office

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Intervallarithmetik

Einführung

Grundrechenarten

Notation

Elementare Funktionen

Intervallerweiterungen allgemeiner Funktionen

Intervallverfahren

Gerundete Intervallarithmetik

Abhängigkeitsproblem und Einhüllungseffekt

Lineare Intervallsysteme

Intervall-Newton Verfahren

Bisektion und Überdeckungen

Anwendung

Rundungsfehleranalyse

Toleranzanalyse

Fuzzy-Arithmetik

Geschichtliches

Implementierungen

Patente

Siehe auch

Referenzen

Literatur

Weblinks

Quellen

What are your Feelings

Share This Article :

Wissen

Automated Chatbot

Data Security

Virtual Reality

Communication

Support

Über uns

Impressum

Datenschutz

Company

About Us

Services

Features

Our Pricing

Latest News