Die Präzession bezeichnet die Richtungsänderung, die die Rotationsachse eines rotierenden Körpers (Kreisel) ausführt, wenn eine äußere Kraft ein Drehmoment senkrecht zu dieser Achse ausübt. Dabei beschreibt die Rotationsachse einen Umlauf auf dem Mantel eines gedachten Kegels mit fester Kegelachse. Anschaulich zeigt sich die Präzession beim Tischkreisel, der trotz Schiefstellung nicht umkippt, solange er rotiert.

Speziell in der Astronomie ist mit Präzession die Richtungsänderung der Erdachse gemeint, die eine Folge der Massenanziehung des Mondes und der Sonne in Verbindung mit der Abweichung der Erdfigur von der Kugelform ist. Über die astronomischen Beobachtungen leitet sich auch der Begriff Präzession her.

Wenn beim rotierenden Kreisel versucht wird seine Rotationsachse zu kippen, dann lässt sich eine Kraftwirkung senkrecht zur Kipprichtung der Rotationsachse registrieren. Je schneller der Kreisel rotiert, desto größer sind die auftretenden Kräfte. Erklären lässt sich das mit dem hohen Drehimpuls des Kreisel, der in seiner Richtung geändert werden muss. Dessen Änderung erfolgt in der Richtung in der die Rotationsachse gekippt wird und erfordert ein Drehmoment das in der Kippebene liegt. Das aufzubringende Drehmoment bedingt die Kraftwirkung senkrecht zur Kipprichtung.

Nun sei ein rotierender Tischkreisel angenommen, der schräg steht. Durch sein Gewicht entsteht dann ein Drehmoment M auf dem Schwerpunkt des Kreisels, das einen normalen Körper umkippen liese. Dabei gibt α den Winkel zwischen Rotationsachse und Schwerkraft an, r ist der Abstand zwischen Auflagepunkt und Schwerpunkt des Kreisel sowie m die Masse und g die Erdbeschleunigung.

Nun ist bekannt das schief stehende Kreisel den charakteristischen Präzessionskegel mit der Symmetrieachse längs der Schwerkraft überstreichen. Daher sei eine Winkelgeschwindigkeit angenommen, mit der die Rotationsachse des Kreisel geschwenkt wird und wodurch das Kreiselmoment M_K auftritt. Diese Winkelgeschwindigkeit sei nun längs der Schwerkraft ausgerichtet und soll einen Betrag aufweisen, das das Drehmoment, wegen dem der Kreisel kippt, aufhebt. L gibt den Drehimpuls des Kreisels an.

Das Kreiselmoment M_K liegt in der Ebene senkrecht zur Schwerkraft und zeigt in die selbe Richtung wie das Drehmoment das den Kreisel kippt. Durch Überführung des Kreuzprodukts in Betragsschreibweise ergibt sich das Kreiselmoment im Betrag und lässt sich mit dem Drehmoment gleichsetzen. Durch Umstellen folgt aus den Kreiseldaten die Winkelgeschwindigkeit der Präzessionsbewegung.

Dabei stellt I_S das Trägheitsmoment dar und ω_S die Winkelgeschwindigkeit des Kreisels. Das Kreiselmoment ist eine Näherungsformel für und so auch die resultierende Formel.

Die resultierende Winkeländerung pro Zeit wird bei der Rotation der Erde als Präzessionskonstante bezeichnet.

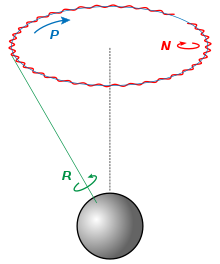
Die Erde hat keine exakte Kugelform, sondern durch die Abplattung des Erdellipsoids von 1:298,25 einen zusätzlichen „Äquatorwulst“ (engl. equatorial bulge) von 21 km. Dadurch bewirken die Gezeitenkräfte von Mond und Sonne ein Drehmoment, welches die Erdachse aufzurichten versucht und zur Präzession der Erdachse führt (auch als Lunisolare Präzession bezeichnet, in der Zeichnung mit P markiert). Die Erdachse beschreibt dadurch einen kegelartigen Umlauf um eine Achse, die rechtwinklig auf der Ekliptikebene steht. Der (nahezu) konstante Winkel zwischen der Erdachse und der Achse des Kegels ist die Schiefe der Ekliptik; er beträgt etwa 23,44°. Für einen vollen Kegelumlauf benötigt die Erdachse um die 25.700–25.800 Jahre. Dieser Zeitraum wird Zyklus der Präzession (auch Platonisches Jahr) genannt und durch die Präzessionskonstante beschrieben.

Auch die Ebene der Mondbahn, die gegenüber der Ekliptik um rund 5° geneigt ist, weist eine Präzessionsbewegung mit einer Periodenlänge von 18,6 Jahren auf; d.h. ihr Normalenvektor beschreibt einen Kegelumlauf mit dieser Umlaufdauer um den Normalenvektor der Ekliptik. Die dadurch verursachte Änderung des Drehmoments hat ebenfalls eine Auswirkung auf die Richtungsänderung der Erdachse: Dem kegelförmigen Präzessionsumlauf überlagert sich eine periodische Abweichung mit einer Amplitude von 9,2" und einer Periode von 18,6 Jahren. Diese nickende Bewegung der Erdachse heißt Nutation. In der Zeichnung ist sie mit N bezeichnet. Daneben gibt es noch weitere Nutationsanteile mit kürzeren Perioden und Amplituden unter 1". (Der hier verwendete astronomische Begriff der Nutation ist nicht identisch mit dem in der Mechanik verwendeten Begriff der Nutation in der Kreiseltheorie.)

Zusammen mit dem Kegelumlauf der Erdachse dreht sich auch die zur Erdachse rechtwinklig liegende Ebene, der Äquator. Dabei dreht sich die zum Frühlingspunkt gerichtete Gerade, in der sich der Äquator mit der Ekliptik unter dem Winkel von derzeit etwa 23,43° schneidet, auf der Ekliptik mit einer Umlaufdauer von ebenfalls rund 25.800 Jahren im Uhrzeigersinn (bei Betrachtung aus der Richtung des nördlichen Poles). Seine Winkelgeschwindigkeit von 360° in 25.800 Jahren oder rund 50" pro Jahr ist die Präzessionskonstante. Der Frühlingspunkt ist eine Bezugsachse sowohl des äquatorialen als auch des ekliptikalen Koordinatensystems, deren räumliche Orientierungen sich somit infolge der Präzession allmählich ändern. Damit ändern sich auch die auf das äquatoriale System bezogenen Koordinaten der Fixsterne. Dieser Effekt ist schon seit über zweitausend Jahren bekannt. Der griechische Astronom Hipparchos verglich etwa um 150 v. Chr. die Sternörter seines neu gemessenen Kataloges mit den Daten aus mehrere hundert Jahre alten Aufzeichnungen und stellte Unterschiede fest. Die Babylonier dürften das Phänomen der Präzession aber schon etwa 170 Jahre früher entdeckt haben. Jedoch erst im 16. Jahrhundert hat Nikolaus Kopernikus die Neigung der Erdachse und ihre Bewegung als Ursache für die Verschiebung des Frühlingspunkts erkannt.^[1]

Die Präzession der Erdachse wirkt sich auch auf die Definition eines Jahres aus. Allgemein versteht man unter einem Jahr den Zeitraum, in dem die in der Ekliptik umlaufende Gerade von der Sonne zur Erde (oder von der Erde zur Sonne) ihre Richtung um 360° (gegen den Uhrzeigersinn, bei Betrachtung aus der Richtung des nördlichen Poles) ändert. Beim siderischen Jahr wird diese Richtungsänderung auf eine Bezugsachse bezogen, die sich nicht entlang der Ekliptik bewegt. Beim tropischen Jahr ist die Bezugsachse dagegen der Frühlingspunkt. Da der Frühlingspunkt selbst sich aufgrund der Präzession der Erdachse mit einer Winkelgeschwindigkeit von 50" pro Jahr im Uhrzeigersinn auf der Ekliptik verlagert, ist die resultierende Winkelgeschwindigkeit der Geraden von der Erde zur Sonne relativ zum Frühlingspunkt etwas größer und damit ein tropisches Jahr etwas kürzer als ein siderisches Jahr. Weil der Frühlingspunkt innerhalb von 25.800 Jahren einen Umlauf von 360° ausführt, ist in diesem Zeitraum die Anzahl der Umläufe der Geraden von der Erde zur Sonne relativ zum Frühlingspunkt um 1 größer als relativ zu einer festen Bezugsachse. Die Differenz zwischen einem tropischen und einem siderischen Jahr summiert sich also in 25.800 Jahren zu einem ganzen Jahr; folglich ist ein tropisches Jahr um ein 25800stel Jahr ≈ 20 Minuten kürzer als ein siderisches Jahr. Für die Jahreszeiten auf der Erde ist nicht die Richtung der Sonne in Bezug auf ein absolut festliegendes Koordinatensystem, sondern in Bezug auf das äquatoriale Koordinatensystem maßgeblich, dessen 3. Achse die präzedierende Erdachse ist; so ist etwa der Frühlingsanfang immer dann, wenn die Sonne in der Richtung des Frühlingspunktes steht, ungeachtet dessen, dass dieser sich langsam bewegt. Deshalb ist das Kalenderjahr durch die geltende Schaltjahrsregelung so festgelegt, dass es sich im langfristigen Mittel gut an das tropische Jahr anpasst.

Gegenwärtig zeigt die Erdachse recht genau in Richtung des Polarsterns, so dass alle Fixsterne scheinbar eine Kreisbahn um ihn beschreiben. Als Folge der Präzession liegt der Himmelspol aber nicht fest beim Polarstern, sondern er wandert auf einem Kreis mit einem Radius von etwa 23,5° (konstante Schiefe der Ekliptik angenommen) um den Ekliptikpol. In 12.000 Jahren wird er sich bei der Wega im Sternbild Leier befinden, dem zweithellsten nördlichen Stern, und das Sternbild „Großer Hund“ beispielsweise wird von Mitteleuropa aus nicht mehr sichtbar sein, vom Sternbild Orion nur noch die sogenannten Schultersterne.

Im Rahmen der Milanković-Zyklen gibt es einen Einfluss der Präzession auf die Eiszeiten, über dessen Ausmaß aber noch Unklarheit herrscht.

• Nutation (Physik) – die nicht durch äußere Kräfte verursachte Bewegung der Achse eines Kreisels
• Nutation (Astronomie) – die Nutation von Himmelskörpern, insbesondere der Erde
• Künstlicher Horizont – wo die Präzession als Störeffekt auftritt
• Präzession des Perizentrums bzw. Perihels – ein Effekt mit anderer physikalischer Ursache

1. ↑ Nicolaus Copernicus: De revolutionibus orbium coelestium, 3. Buch, Kapitel 1

• Präzession der Erdachse in der Astronomie-Bibliothek auf Astronomie.de
• Präzession eines seitlich von seinem Schwerpunkt aufgehängten rotierenden Rades
• animierte Java-Simulation des einseitig unterstützten Kreisels mit sämtlichen Parametern (Anfangsbedingungen, Präzession, Nutation, Reibung am Aufstandspunkt, Reibung in der Kreiselachse)