„Rasterung“ – Versionsunterschied

Bei der Rasterung einer Vektorgrafik, in diesem Beispiel im SVG-Format, müssen die Pixel-Farbwerte der resultierenden Rastergrafik ermittelt werden.

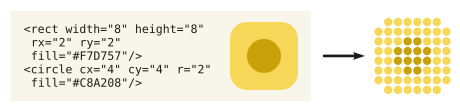
In der 2D-Computergrafik bezeichnet Rasterung, auch Rendern oder Scankonvertierung genannt, die Umwandlung einer Vektor- in eine Rastergrafik.

Verfahren

PDF-Renderer, der Vektorschrift in Pixelgrafik umsetzt. Oben Sumatra PDF, unten Adobe Reader.

Es gibt eine Vielzahl von Algorithmen zur Rasterung von grafischen Primitiven, wie Linien, Polygonen, Kreisen und anderen geometrischen Formen, siehe dazu:

Ein bekanntes Problem der Rasterung ist der Treppeneffekt. Steht für die zu erzeugende Rastergrafik eine Farbtiefe von mehr als 1 Bit pro Pixel zur Verfügung, so kann dieser Effekt mittels Kantenglättung (Antialiasing) vermindert werden. Dazu gibt es mehrere Methoden, die teils ungewichtet arbeiten, teils einen speziellen Rekonstruktionsfilter verwenden. Bei der Rasterung von Text treten spezielle Probleme auf, die mittels Hinting vermieden werden können.

Rasterung dicker Primitiven

Bei der Rasterung von grafischen Primitiven mit einer bestimmten Dicke gibt es, sofern sie nicht bereits vom verwendeten Antialiasing-Algorithmus unterstützt wird, mehrere Möglichkeiten. Bei Polygonen müssen hierbei auch die Verbindungsstellen zwischen den einzelnen Liniensegmenten beachtet werden, siehe hierzu Rasterung von Polygonen.

Pixelwiederholung: Eine Methode ist, bei der Rasterung anstatt eines mehrere Pixel vertikal bzw. horizontal zu zeichnen. Ein Problem ist, dass Kurvenenden bei dicken Kurven „abgeschnitten“ wirken. Daneben kann es an den Stellen, an denen von horizontaler zu vertikaler Wiederholung oder umgekehrt gewechselt wird, zu merklichen Lücken kommen. Außerdem weisen derartig gerasterte Kurven, ähnlich wie dünne Linien, eine unterschiedliche Dicke in Abhängigkeit von der lokalen Steigung auf.
Pinsel: Hierbei wird eine bestimmte Rastergrafik als „Pinsel“, im einfachsten Fall ein Quadrat mit gewünschter Kantenlänge, entlang der Kurve bewegt. Auch hier variiert die Dicke in Abhängigkeit von der Steigung, im Gegensatz zur Pixelwiederholung ist die Linie jedoch bei Diagonalschritten am dicksten. Dieses Problem lässt sich dadurch umgehen, dass das Quadrat gemäß der lokalen Steigung der Kurve gedreht wird, einfacher ist es jedoch, einen Kreis als Pinsel zu verwenden. Ein Nachteil der Methode ist, dass man bei der Rasterung auf sehr viele bereits in den vorhergehenden Schritten eingefärbte Pixel stößt. Dieser Effekt ist umso größer, je dicker die Kurve ist. Um das Problem der variierenden Kurvendicke zu lösen, können polygonförmige Pinsel verwendet werden.^[1]
Füllen zwischen Rändern: Eine andere Methode zur Rasterung einer dicken Kurve besteht darin, ihre beiden Ränder in einigem Abstand voneinander zu zeichnen und den dazwischen liegenden Bereich auszufüllen. Ein Nachteil ist, dass bei der zweifarbigen Rasterung die Kurve wegen Rundungsfehlern möglicherweise etwas verschoben erscheint. Bei Ellipsen muss beachtet werden, dass die Rasterung durch das Zeichnen zweier konfokaler Ellipsen mit unterschiedlich langen Halbachsen geometrisch nicht korrekt ist.
Liniensegmente: Schließlich gibt es die Möglichkeit, dicke Kurven durch eine Aneinanderreihung kurzer Liniensegmente zu zeichnen. Dabei müssen die gleichen Besonderheiten wie bei der Rasterung von Polygonen beachtet werden, damit die Liniensegmente korrekt miteinander verbunden werden.

Löschung von Primitiven

Bereits gezeichnete Figuren können selektiv gelöscht werden, indem sie nochmals mit der Hintergrundfarbe gezeichnet werden. Das funktioniert jedoch nicht, wenn sie andere Figuren überschneiden, da hierbei auch unerwünschte Bildteile gelöscht werden können. Eine effiziente Möglichkeit, dies zu vermeiden, sind Minimax- oder Boxing-Tests. Hierbei wird zunächst geprüft, ob sich in dem von der zu löschenden Figur aufgespannten Rechteck andere Figuren befinden. Nur wenn dies der Fall ist, muss auf Schnittpunkte getestet und gegebenenfalls der gesamte Bereich neu gezeichnet werden.

3D-Rasterung

Raytracing und Rasterung sind zwei grundlegend unterschiedliche Ansätze zum Rendern von Bildern von 3D-Szenen angesehen, obwohl sie für Primärstrahlen dieselben Ergebnisse berechnen. Durch die Rasterung wird jedes Dreieck auf die Bildebene projiziert und alle abgedeckten Pixel in 2D aufgelistet, während die Strahlverfolgung in 3D ausgeführt wird, indem Strahlen durch jedes Pixel erzeugt und dann der nächstgelegene Schnittpunkt mit einem Dreieck gefunden werden.

Man kann die Anwendung einer Modell- oder Ansichtstransformation vermeiden, indem man stattdessen den Sampler-Generator transformiert. Während beim Raytracing normalerweise Gleitkommazahlen mit seinen numerischen Problemen verwendet werden, kann 3D-Rasterung mit denselben Konsistenzregeln wie die 2D-Rasterung implementiert werden kann. Bei der 3D-Rasterung bestehen die einzigen verbleibenden Unterschiede zwischen den beiden Ansätzen in der Szenenüberquerung und der Aufzählung potenziell abgedeckter Samples auf der Bildebene (siehe Binning).

Berechnungen

Um zu herauszufinden, ob ein Pixel der Bildebene von einem Dreieck bedeckt wird, reicht es, zu prüfen, ob der Projektionsstrahl (siehe Zentralprojektion), der durch das Pixel verläuft, das Dreieck schneidet.

Nimmt man an, dass das Projektionszentrum ${\vec {e}}$ der Koordinatenursprung des dreidimensionalen kartesischen Koordinatensystems ist, und bezeichnet die Ecken des projizierten Dreiecks mit ${\vec {p_{0}}}$ , ${\vec {p_{1}}}$ , ${\vec {p_{2}}}$ , dann ergibt sich folgende Bedingungen dafür, dass das Pixel im projizierten Dreieck liegt:

Die Ebene, die durch das Dreieck $({\vec {e}},{\vec {p_{1}}},{\vec {p_{0}}})$ verläuft, teilt den dreidimensionalen Raum in zwei Halbräume. Das Pixel der Bildebene muss in dem Halbraum liegen, in dem sich der Punkt ${\vec {p_{2}}}$ befindet. Außerdem muss das Pixel
in dem durch das Dreieck $({\vec {e}},{\vec {p_{2}}},{\vec {p_{1}}})$ definierten Halbraum liegen, in dem sich der Punkt ${\vec {p_{0}}}$ befindet und
in dem durch das Dreieck $({\vec {e}},{\vec {p_{0}}},{\vec {p_{2}}})$ definierten Halbraum liegen, in dem sich der Punkt ${\vec {p_{1}}}$ befindet.

Um zu prüfen, ob sich ein Punkt ${\vec {p}}$ in einem durch die Punkte ${\vec {a}}$ , ${\vec {b}}$ und ${\vec {c}}$ definierten Halbraum befindet, kann man folgende Funktion verwenden:

V({\vec {p}}):={\vec {n}}\cdot {\vec {p}}=(({\vec {b}}-{\vec {a}})\times ({\vec {c}}-{\vec {b}}))\cdot {\vec {p}}

wobei ${\vec {n}}\cdot {\vec {p}}$ das Skalarprodukt der Vektoren ${\vec {n}}$ und ${\vec {p}}$ ist. Der Normalenvektor ${\vec {n}}$ ist durch das Kreuzprodukt

{\vec {n}}:=({\vec {b}}-{\vec {a}})\times ({\vec {c}}-{\vec {b}})

definiert. Diese Funktion berechnet das Volumen des Tetraders mit den Ecken ${\vec {a}}$ , ${\vec {b}}$ , ${\vec {c}}$ , ${\vec {p}}$ . Wenn der Punkt ${\vec {p}}$ oberhalb des Dreiecks $({\vec {a}},{\vec {b}},{\vec {c}})$ liegt, ist das Vorzeichen positiv, wenn ${\vec {p}}$ unterhalb liegt, ist das Vorzeichen negativ. Wenn ${\vec {p}}$ in der Ebene des Dreiecks $({\vec {a}},{\vec {b}},{\vec {c}})$ liegt, ist das Volumen gleich 0.

Mit den Funktionen

V_{0}({\vec {d}}):=({\vec {p_{2}}}-{\vec {e}})\times ({\vec {p_{1}}}-{\vec {p_{2}}})

V_{1}({\vec {d}}):=({\vec {p_{0}}}-{\vec {e}})\times ({\vec {p_{2}}}-{\vec {p_{0}}})

V_{2}({\vec {d}}):=({\vec {p_{1}}}-{\vec {e}})\times ({\vec {p_{0}}}-{\vec {p_{1}}})

kann folgende Aussage formuliert werden:

Das Pixel ${\vec {d}}$ liegt genau dann im projizierten Dreieck, wenn $V_{0}({\vec {d}})>0$ und $V_{1}({\vec {d}})>0$ und $V_{2}({\vec {d}})>0$ ist.

Der Schnittpunkt ${\vec {e}}+t\cdot {\vec {d}}$ des Pixels ${\vec {d}}$ mit dem ursprünglichen Dreieck $({\vec {p_{0}}},{\vec {p_{1}}},{\vec {p_{2}}})$ kann auch mit baryzentrischen Koordinaten der Punkte ${\vec {p_{0}}}$ , ${\vec {p_{1}}}$ , ${\vec {p_{2}}}$ ausgedrückt werden. Dann gilt:

{\vec {e}}+t\cdot {\vec {d}}=t\cdot {\vec {d}}=\lambda _{0}\cdot {\vec {p_{0}}}+\lambda _{1}\cdot {\vec {p_{1}}}+\lambda _{2}\cdot {\vec {p_{2}}}

mit

\lambda _{i}={\frac {V_{i}({\vec {d}})}{V_{0}({\vec {d}})+V_{1}({\vec {d}})+V_{2}({\vec {d}})}}

wobei $t$ und die $\lambda _{i}$ reelle Zahlen sind. Die baryzentrischen Koordinaten werden mit ${\vec {e}}+t\cdot {\vec {d}}=(\lambda _{0}:\lambda _{1}:\lambda _{2})$ bezeichnet.^[2]

Literatur

James D. Foley u. a.: Computer Graphics: Principles and Practice. Addison-Wesley, Reading 1995, ISBN 0-201-84840-6
David F. Rogers: Procedural Elements for Computer Graphics. WCB/McGraw-Hill, Boston 1998, ISBN 0-07-053548-5

Weblinks

Commons: Rasterung – Sammlung von Bildern, Videos und Audiodateien

Grundlagen der Computergrafik – Rasterisierung. Archiviert vom Original am 6. August 2016; abgerufen am 9. November 2017.

Einzelnachweise

↑ John D. Hobby: Digitized Brush Trajectories. Dissertation, Stanford University, 1985 (PDF, 30 MB (Memento des Originals vom 26. Oktober 2006 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/cm.bell-labs.com)
↑ 3D Rasterization: A Bridge between Rasterization and Ray Casting

[1] John D. Hobby: Digitized Brush Trajectories. Dissertation, Stanford University, 1985 (PDF, 30 MB (Memento des Originals vom 26. Oktober 2006 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/cm.bell-labs.com)

[2] 3D Rasterization: A Bridge between Rasterization and Ray Casting

[1]

[2]

@@ Zeile 1: / Zeile 1: @@
 {{Begriffsklärungshinweis|Für den Begriff in der Drucktechnik siehe [[Druckraster]].}}
-[[Datei:Scan-conversion.svg|mini|hochkant=2.1|Bei der Rasterung einer Vektorgrafik, in diesem Beispiel im [[Scalable Vector Graphics|SVG]]-Format, müssen die Pixel-Farbwerte der resultierenden Rastergrafik ermittelt werden.]]
+[[Datei:Scan-conversion.svg|mini|hochkant=2.1|Bei der Rasterung einer [[Vektorgrafik]], in diesem Beispiel im [[Scalable Vector Graphics|SVG]]-Format, müssen die Pixel-Farbwerte der resultierenden [[Rastergrafik]] ermittelt werden.]]
 In der 2D-[[Computergrafik]] bezeichnet '''Rasterung''', auch ''Rendern'' oder ''Scankonvertierung'' genannt, die Umwandlung einer [[Vektorgrafik|Vektor]]- in eine [[Rastergrafik]].
 == Verfahren ==
-[[Datei:textrenderp2.png|mini|[[Portable Document Format|PDF]]-Renderer, der Vektorschrift in Pixelgrafik umsetzt. Oben [[Sumatra PDF]], unten [[Adobe Reader]].]]
+[[Datei:textrenderp2.png|mini|[[Portable Document Format|PDF]]-Renderer, der [[Vektorschrift]] in [[Pixelgrafik]] umsetzt. Oben [[Sumatra PDF]], unten [[Adobe Reader]].]]
 Es gibt eine Vielzahl von [[Algorithmus|Algorithmen]] zur Rasterung von [[Grafisches Primitiv|grafischen Primitiven]], wie Linien, [[Polygon]]en, [[Kreis]]en und anderen [[Geometrisch|geometrischen]] Formen, siehe dazu:
@@ Zeile 29: / Zeile 29: @@
 [[Raytracing]] und Rasterung sind zwei grundlegend unterschiedliche Ansätze zum [[Rendern (Bildsynthese)|Rendern]] von Bildern von [[3D]]-Szenen angesehen, obwohl sie für Primärstrahlen dieselben Ergebnisse berechnen. Durch die Rasterung wird jedes [[Dreieck]] auf die [[Bildebene (darstellende Geometrie)|Bildebene]] projiziert und alle abgedeckten Pixel in [[2D]] aufgelistet, während die Strahlverfolgung in 3D ausgeführt wird, indem [[Strahl (Geometrie)|Strahlen]] durch jedes [[Pixel]] erzeugt und dann der nächstgelegene [[Schnittpunkt]] mit einem Dreieck gefunden werden.
-Man kann die Anwendung einer Modell- oder Ansichtstransformation vermeiden, indem man stattdessen den Sampler-Generator transformiert. Während beim [[Raytracing]] normalerweise [[Gleitkommazahl]]en mit seinen numerischen Problemen verwendet werden, kann [[3D]]-Rasterung mit denselben Konsistenzregeln wie die [[2D]]-Rasterung implementiert werden kann. Bei der 3D-Rasterung bestehen die einzigen verbleibenden Unterschiede zwischen den beiden Ansätzen in der Szenenüberquerung und der Aufzählung potenziell abgedeckter Samples auf der [[Bildebene (darstellende Geometrie)|Bildebene]] (siehe [[Binning]]).<ref>[http://cg.ivd.kit.edu/publications/p2012/3dr/gi2012.pdf 3D Rasterization: A Bridge between Rasterization and Ray Casting]</ref>
+Man kann die Anwendung einer Modell- oder Ansichtstransformation vermeiden, indem man stattdessen den Sampler-Generator transformiert. Während beim [[Raytracing]] normalerweise [[Gleitkommazahl]]en mit seinen numerischen Problemen verwendet werden, kann [[3D]]-Rasterung mit denselben Konsistenzregeln wie die [[2D]]-Rasterung implementiert werden kann. Bei der 3D-Rasterung bestehen die einzigen verbleibenden Unterschiede zwischen den beiden Ansätzen in der Szenenüberquerung und der Aufzählung potenziell abgedeckter Samples auf der [[Bildebene (darstellende Geometrie)|Bildebene]] (siehe [[Binning]]).
+=== Berechnungen ===
+Um zu herauszufinden, ob ein [[Pixel]] der [[Bildebene (darstellende Geometrie)|Bildebene]] von einem [[Dreieck]] bedeckt wird, reicht es, zu prüfen, ob der Projektionsstrahl (siehe [[Zentralprojektion]]), der durch das [[Pixel]] verläuft, das Dreieck schneidet.
+Nimmt man an, dass das Projektionszentrum <math>\vec e</math> der [[Koordinatenursprung]] des [[Dreidimensional|dreidimensionalen]] [[Kartesisches Koordinatensystem|kartesischen Koordinatensystems]] ist, und bezeichnet die [[Ecke|Ecken]] des projizierten [[Dreieck|Dreiecks]] mit <math>\vec{p_0}</math>, <math>\vec{p_1}</math>, <math>\vec{p_2}</math>, dann ergibt sich folgende Bedingungen dafür, dass das Pixel im projizierten Dreieck liegt:
+* Die [[Ebene (Mathematik)|Ebene]], die durch das Dreieck <math>(\vec e, \vec{p_1}, \vec{p_0})</math> verläuft, teilt den [[Dreidimensional|dreidimensionalen]] [[Raum (Mathematik)|Raum]] in zwei [[Halbraum|Halbräume]]. Das Pixel der [[Bildebene (darstellende Geometrie)|Bildebene]] muss in dem Halbraum liegen, in dem sich der [[Punkt (Geometrie)|Punkt]] <math>\vec{p_2}</math> befindet. Außerdem muss das [[Pixel]]
+* in dem durch das Dreieck <math>(\vec e, \vec{p_2}, \vec{p_1})</math> definierten Halbraum liegen, in dem sich der Punkt <math>\vec{p_0}</math> befindet und
+* in dem durch das Dreieck <math>(\vec e, \vec{p_0}, \vec{p_2})</math> definierten Halbraum liegen, in dem sich der Punkt <math>\vec{p_1}</math> befindet.
+Um zu prüfen, ob sich ein [[Punkt (Geometrie)|Punkt]] <math>\vec p</math> in einem durch die Punkte <math>\vec a</math>, <math>\vec b</math> und <math>\vec c</math> definierten [[Halbraum]] befindet, kann man folgende [[Funktion (Mathematik)|Funktion]] verwenden:
+:<math>V(\vec p) := \vec n \cdot \vec p = ((\vec b - \vec a) \times (\vec c - \vec b)) \cdot \vec p</math>
+wobei <math>\vec n \cdot \vec p</math> das [[Skalarprodukt]] der [[Vektor|Vektoren]] <math>\vec n</math> und <math>\vec p</math> ist. Der [[Normalenvektor]] <math>\vec n</math> ist durch das [[Kreuzprodukt]]
+:<math>\vec n := (\vec b - \vec a) \times (\vec c - \vec b)</math>
+definiert. Diese Funktion berechnet das [[Volumen]] des [[Tetraeder|Tetraders]] mit den [[Ecke|Ecken]] <math>\vec a</math>, <math>\vec b</math>, <math>\vec c</math>, <math>\vec p</math>. Wenn der [[Punkt (Geometrie)|Punkt]] <math>\vec p</math> oberhalb des [[Dreieck|Dreiecks]] <math>(\vec a, \vec b, \vec c)</math> liegt, ist das [[Vorzeichen (Zahl)|Vorzeichen]] positiv, wenn <math>\vec p</math> unterhalb liegt, ist das Vorzeichen negativ. Wenn <math>\vec p</math> in der [[Ebene (Mathematik)|Ebene]] des Dreiecks <math>(\vec a, \vec b, \vec c)</math> liegt, ist das Volumen gleich 0.
+Mit den [[Funktion (Mathematik)|Funktionen]]
+:<math>V_0(\vec d) := (\vec{p_2} - \vec e) \times (\vec{p_1} - \vec{p_2})</math>
+:<math>V_1(\vec d) := (\vec{p_0} - \vec e) \times (\vec{p_2} - \vec{p_0})</math>
+:<math>V_2(\vec d) := (\vec{p_1} - \vec e) \times (\vec{p_0} - \vec{p_1})</math>
+kann folgende Aussage formuliert werden:
+* Das Pixel <math>\vec d</math> liegt genau dann im projizierten [[Dreieck]], wenn <math>V_0(\vec d) > 0</math> und <math>V_1(\vec d) > 0</math> und <math>V_2(\vec d) > 0</math> ist.
+Der [[Schnittpunkt]] <math>\vec e + t \cdot \vec d</math> des Pixels <math>\vec d</math> mit dem ursprünglichen Dreieck <math>(\vec{p_0}, \vec{p_1}, \vec{p_2})</math> kann auch mit [[Baryzentrische Koordinaten|baryzentrischen Koordinaten]] der Punkte <math>\vec{p_0}</math>, <math>\vec{p_1}</math>, <math>\vec{p_2}</math> ausgedrückt werden. Dann gilt:
+:<math>\vec e + t \cdot \vec d = t \cdot \vec d = \lambda_0 \cdot \vec{p_0} + \lambda_1 \cdot \vec{p_1} + \lambda_2 \cdot \vec{p_2} </math> mit <math>\lambda_i = \frac{V_i(\vec d)}{V_0(\vec d) + V_1(\vec d) + V_2(\vec d)} </math>
+wobei <math>t</math> und die <math>\lambda_i</math> [[Reelle Zahl|reelle Zahlen]] sind. Die baryzentrischen Koordinaten werden mit <math>\vec e + t \cdot \vec d = (\lambda_0 : \lambda_1 : \lambda_2)</math> bezeichnet.<ref>[http://cg.ivd.kit.edu/publications/p2012/3dr/gi2012.pdf 3D Rasterization: A Bridge between Rasterization and Ray Casting]</ref>
 == Literatur ==

Land Bayern

„Rasterung“ – Versionsunterschied

Version vom 19. September 2020, 22:55 Uhr

Inhaltsverzeichnis

Verfahren

Rasterung dicker Primitiven

Löschung von Primitiven

3D-Rasterung

Berechnungen

Literatur

Weblinks

Einzelnachweise

What are your Feelings

„Rasterung“ – Versionsunterschied

Version vom 19. September 2020, 22:55 Uhr

Verfahren

Rasterung dicker Primitiven

Löschung von Primitiven

3D-Rasterung

Berechnungen

Literatur

Weblinks

Einzelnachweise

What are your Feelings

Share This Article :