Chaosforschung

Die Chaosforschung ist ein Teilgebiet der Mathematik und Physik und befasst sich im Wesentlichen mit Systemen, deren Dynamik unter bestimmten Bedingungen empfindlich von den Anfangsbedingungen abhängt, so dass ihr Verhalten nicht langfristig vorhersagbar ist. Da diese Dynamik einerseits den physikalischen Gesetzen unterliegt, andererseits aber irregulär erscheint, bezeichnet man sie als deterministisches Chaos. Chaotische Systeme sind nichtlineare dynamische Systeme. Beispiele sind der Schmetterlingseffekt beim Wetter, Turbulenzen, Wirtschaftskreisläufe, bestimmte Musterbildungsprozesse, wie beispielsweise Erosion, sowie neuronale Netze und damit letztlich auch menschliches Verhalten.

Die Chaosforschung wurde bei ihrem Aufkommen von der Öffentlichkeit mit großem Interesse verfolgt. Die damit verbundenen oft überhöhten Erwartungen hat sie jedoch nicht erfüllen können. So wird der in der Öffentlichkeit populäre Begriff Chaostheorie in Fachkreisen eher vermieden. Die Erfolge der Chaosforschung bestehen im Wesentlichen in der Entdeckung bestimmter universeller Strukturen und Prinzipien im scheinbar regellosen Verhalten chaotischer Systeme wie beispielsweise der Periodenverdopplung beim Übergang ins Chaos und den so genannten seltsamern Attraktoren.

Die Chaosforschung basiert unter anderem auf Arbeiten von Henri Poincaré, Edward N. Lorenz, Benoit Mandelbrot und Mitchell Feigenbaum. Die hier dargestellten Phänomene entsprechen den Minimalkonsens darüber, was thematisch zur Chaosforschung zählt.

Grundlagen

Anders als der Begriff Chaos in der Umgangssprache charakterisiert deterministisches Chaos nicht den Zustand eines Systems, wie beispielsweise seine Unordnung, sondern sein zeitliches Verhalten, das heißt seine Dynamik. Chaotisches Verhalten liegt dann vor, wenn selbst geringste Änderungen der Anfangsbedingungen nach einer gewissen Zeit zu einem völlig anderen Verhalten führen. Das ist genau dann der Fall, wenn die entsprechenden Unterschiede in der zeitlichen Entwicklung eines Systems zunächst exponentiell mit der Zeit anwachsen anstatt linear oder polynomial, das System aber beschränkt ist, so dass dem Wachstum dieser Unterschiede eine Grenze gesetzt ist. Es stellt sich ein nichtperiodisches und scheinbar irreguläres Verhalten ein.

Grenzen der Vorhersagbarkeit

Die Anforderungen an die Präzision der Kenntnis der Anfangsbedingungen für die Vorhersage des Verhaltens für einen bestimmten Zeitraum übersteigt daher rasch die Möglichkeiten praktischer Messgenauigkeit um astronomische Faktoren. So kann beispielsweise der Zustand im Gerät zur Ziehung der Lottozahlen mit Kugeln nach einigen Dutzend Stößen schon durch die zusätzliche Gravitationswechselwirkung mit einem Elektron am Rande des sichtbaren Universums ein völlig anderer sein. Dieses Phänomen ist auch unter dem Schlagwort Schmetterlingseffekt in der Öffentlichkeit bekannt geworden, wonach selbst der Flügelschlag eines Schmetterlings auf lange Sicht zu einem anderem Ablauf des Wettergeschehens führen kann. Obwohl solche Systeme im Rahmen der klassischen Physik an sich dem Determinismus unterliegen, ist eine praktische Vorhersage prinzipiell nur für mehr oder weniger kurze Zeitspannen möglich.

Schwache und starke Kausalität

Man unterscheidet in der Physik zwischen dem Prinzip der schwachen und der starken Kausalität:

  • Schwache Kausalität bedeutet, dass sich identisch präparierte Systeme identisch verhalten.
  • Starke Kausalität bedeutet, dass sich hinreichend ähnlich präparierte Systeme ähnlich verhalten.

Das Prinzip der schwachen Kausalität ist zwar in den Gesetzen der klassischen Physik verankert, es ist aber nicht in dieser Strenge überprüfbar, da aufgrund von unvermeidlichen Messfehlern zwei Systeme nicht absolut identisch präpariert werden können. Dagegen ist das Prinzip der starken Kausalität die Grundlage des Erfolges der experimentellen Naturwissenschaften. Bei chaotischen Systemen ist aber das Prinzip der starken Kausalität bei hinreichend langen Beobachtungszeiträumen nicht erfüllt. Ähnliche Ausgangszustände können zu völlig verschiedenem Verhalten führen.

Quantentheorie und Determinismus

Die Berücksichtigung der Erkenntnisse der Quantentheorie zeigt, dass die Vorhersagbarkeit chaotischer Systeme nicht nur an der Grenze der praktisch möglichen Messgenauigkeit scheitert, sondern dass ihr Verhalten prinzipiell nicht determiniert ist. So besagt die heisenbergsche Unschärferelation, dass Ort und Geschwindigkeit eines Objektes nicht gleichzeitig beliebig genau definiert sind. Diese Einschränkung bezieht sich nicht auf Unzulänglichkeiten des Beobachtungsvorgangs sondern ist prinzipieller Natur. Diese Unschärfe ist bei makroskopischen Systemen gewöhnlich vernachlässigbar. Da sie bei chaotischen Systemen jedoch exponentiell anwächst, nimmt sie früher oder später makroskopische Dimensionen an. Bei dem Gerät zur Ziehung der Lottozahlen mit Kugeln ist das bereits nach etwa 20 Stößen der Fall. Die Vorhersagbarkeit chaotischer Systeme scheitert daher spätestens an der Unschärferelation. Das bedeutet, dass chaotische Systeme aufgrund der begrenzten Gültigkeit der klassischen Physik prinzipiell nicht deterministisch sind, so wie es auch in der Quantenphysik hinsichtlich der Vorhersage bestimmter Messergebnisse der Fall ist.

Nichtlineare Systeme

Chaotisches Verhalten kann nur in Systemen auftreten, deren Dynamik durch nichtlineare Gleichungen beschrieben wird. Solche Gleichungen sind meist nicht analytisch, d. h. in Form einer Formel, sondern nur numerisch lösbar. Ursache des exponentiellen Wachstums von Unterschieden in den Anfangsbedingungen sind dabei oft Mechanismen von Selbstverstärkung beispielsweise durch Rückkopplungen. Ist durch Reibung hinreichend Dissipation im Spiel, so kann sich kein chaotisches Verhalten ausbilden. So könnten beispielsweise bei Jahrmarktsfahrgeschäften, die konstruktionsbedingt zu chaotischen Verhalten neigen, ohne entsprechende Bremsmaßnahmen unerwartete und unzumutbare Beschleunigungsspitzen auftreten,

Ljapunow-Exponent

Mathematisch wird die Geschwindigkeit dieses exponentiellen Wachstums durch Ljapunow-Exponenten beschrieben. Dazu betrachtet man die n Zustandsgrößen xi mit i=1 bis n, die den Zustand des Systems vollständig beschreiben. Ein Unterschied Δxi zwischen zwei nahezu identisch präparierten, gleichartigen Systemen wächst dann von einem Anfangszeitpunkt t=0 ausgehend vereinfacht betrachtet entsprechend

an, wobei λi der Ljapunow-Exponent zu xi ist. Für ein exponentielles Wachstum ist daher mindestens ein positiver Ljapunow-Exponent λi erforderlich.

Diskrete Systeme

Bisher wurde nur das zeitliche Verhalten kontinuierlicher physikalischer Systeme betrachtet. Chaos wird jedoch auch in Modellen studiert, bei denen jeder Zustand durch einen Iterationsschritt diskret in den Folgezustand übergeht. Beispiele sind die logistische Gleichung oder die Iterationsvorschrift, die zur Mandelbrot-Menge führt, die unter der Bezeichnung Apfelmännchen bekannt wurde. Dabei können die gleichen Grundphänomene wie bei kontinuierlichen Systemen auftreten.

Im Prinzip lässt sich einem kontinuierlichen System durch die Betrachtung bestimmter aufeinanderfolgender Zuständen stets ein diskretes System zuordnen. Ein Verfahren ist die sogenannte Poincaré-Abbildung mit der Henri Poincaré Ende des 19. Jahrhunderts die Stabilität der Planetenbewegung studierte.

Phänomene

Ein wesentliches Ergebnis der Chaosforschung ist die Entdeckung, dass chaotische Systeme trotz ihres langfristig nicht vorhersagbaren, scheinbar irregulären Verhalten bestimmte typische Verhaltensmuster zeigen. Da sie bei völlig unterschiedlichen Systeme beobachtet werden, sind sie von universeller Bedeutung.

Seltsame Attraktoren

Ein typisches Phänomen bei chaotischen Prozessen sind sogenannte seltsame Attraktoren. Für ihr Verständnis betrachtet man die Dynamik des Systems anhand von sogenannten Phasendiagrammen.

Phasendiagramme

Phasendiagramme bieten einen anschaulichen Überblick über die Dynamik eines Systems. Der Zustand des Systems wird dabei zu jedem Zeitpunkt durch einen Punkt in einem Raum dargestellt, dessen Koordinatenachsen durch den Satz von unabhängigen Zustandsgrößen des Systems und deren Geschwindigkeiten gegeben sind. Die Dynamik lässt sich damit als die Bahn dieses Punktes im Phasenraum interpretieren. So wird beispielsweise der Phasenraum eines Pendels durch den Auslenkwinkel und die zugehörige Winkelgeschwindigkeit aufgespannt, und eine periodische Pendelbewegung entspricht einer geschlossenen Kurve um den Koordinatenursprung. Mathematisch lässt sich die Gesamtheit aller möglichen Verhaltensweisen als Strömungsfeld im Phasenraum interpretieren.

Attraktoren

In manchen Fällen streben Systeme mit verschiedenen Anfangsbedingungen zu dem selben Verhalten. Die zugehörigen Bahnen im Phasenraum konvergieren dann zu einer bestimmten Bahn, die als Attraktor bezeichnet wird. Im Falle eines freien Pendel mit Reibung wäre das der Ruhezustand, das heißt der Koordinatenursprung im Phasendiagramm, zu dem alle Bahnen spiralförmig hinstreben. In diesem Fall handelt es sich um einen punktförmigen Attraktor, einen Fixpunkt. Attraktoren könne jedoch auch Kurven sein, wie beispielsweise der periodische Grenzzyklus, der sich bei einem Pendel mit Reibung einstellt, das durch eine äußere periodische Kraft zu Schwingungen angeregt wird. Dieses Verhalten ist typisch für dissipative Systeme. Mathematisch betrachtet können Attraktoren immer dann auftreten, wenn die Divergenz des Strömungsfeldes in Bereichen des Phasenraum negativ ist.

Der seltsame Attraktor

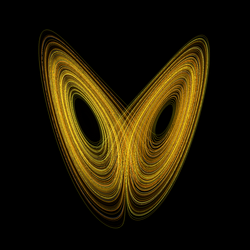
Lorenz-Attraktor in einem dreidimensionalen Phasenraum, dem ein einfaches Wettermodell zugrunde liegt. Der Bahnpunkt kreist links im Uhrzeigersinn und recht entgegen. Bei jedem Umlauf verbreitert sich das Band der Bahnen auf das Doppelte und wird anschließend bei der Abwärtsbewegung in der Bildmitte in zwei Hälften zerschnitten, wobei die Entscheidung fällt, ob der nächste Umlauf links oder rechts stattfindet. Auf diesem Mechanismus beruht der chaotische Charakter der Bahnen.

Chaotische Systeme können nun eine besondere Form von Attraktoren haben, die als seltsame Attraktoren bezeichnet werden. Obwohl sie sich in einem begrenzten Gebiet des Phasenraumes aufhalten, sind sie unendlich lang und nicht periodisch. Bezüglich kleiner Störungen zeigen sie chaotisches Verhalten. Es sind Fraktale mit einer komplizierten und scheinbar irregulären inneren geometrischen Struktur. Sie sind in eine Teilmenge des Phasenraums eingebettet, die eine niedrigere Dimensionalität besitzt als der Phasenraum selbst. Das bedeutet, dass in der Dynamik trotz des chaotischen Charakters nur ein infinitesimaler und damit verschwindender Bruchteil aller möglichen Zustände vorkommt. Der Attraktor selbst hat, wie bei Fraktalen üblich, eine fraktale Dimension, die durch eine gebrochenen Zahl dargestellt wird, und die damit noch kleiner als die Dimension des Einbettungsbereiches ist.

Das bekannteste Beispiel für einen seltsamen Attraktor ist der Lorenz-Attraktor, den Lorenz bei der Modellierung des Wettergeschehens entdeckte. Ein weiteres Beispiel ist der Rössler-Attraktor, auf den Otto Rössler durch die Betrachtung einer Bonbonknetmaschine stieß.

Nach dem Poincaré–Bendixson-Theorem können seltsame Attraktoren erst in Phasenräumen ab drei Dimensionen auftreten. Ursache ist der Umstand, dass Bahnen im Phasenraum, wie bei einem Strömungsfeld üblich, sich nicht kreuzen, was aber für ein chaotisches Verhalten in zwei Dimensionen erforderlich wäre. Seltsame Attraktoren können nur dann auftreten, wenn mindestes ein Ljapunow-Exponent negativ und mindestens einer positiv ist. Der negative sorgt in gewissem Sinne für Konvergenz bezüglich einer Dimension und damit für die Reduktion der Dimensionalität, der positive für das chaotische Verhalten.

Schnittflächen durch den Phasenraum, die senkrecht von Bahnen durchstoßen werden, werden als Poincaré-Abbildung bezeichnet. Im Fall von seltsamen Attraktoren bilden die Durchstoßpunkte Cantor-Mengen.

Auch bei diskreten chaotischen Systeme werden seltsame Attraktoren beobachtet wie beispielsweise der Hénon-Attraktor. Analog zu attraktiven Strukturen können auch repulsive Strukturen auftreten, die ebenfalls fraktal sind, wie beispielsweise die Julia-Mengen.

Der Übergang ins Chaos

Nichtlineare dynamische Systeme können neben Chaos auch andere Verhaltensweisen zeigen, wie beispielsweise Konvergenz gegen einen Ruhezustand oder gegen einen periodischen Grenzzyklus. Welches Verhalten auftritt, kann von den Anfangsbedingungen oder auch von anderen Kontrollparametern abhängen. Eine grafische Darstellung der entsprechenden Einzugsgebiete für bestimmte Verhaltensweisen als Funktion dieser Parameter ist oft fraktal. Der Übergangsbereich zu chaotischem Verhalten zeichnet sich dabei durch bestimmte Eigenschaften aus, wie beispielsweise plötzliche qualitative Änderungen des Verhaltens, die auch als Bifurkation bezeichnet werden.

Periodenverdopplung

Bifurkationsdiagramm der Zahlenfolge zur logistischen Gleichung. Dargestellt sind die Häufungspunkte x der Folge als Funktion des Kontrollparameters r. Links konvergiert die Folge, rechts ist sie chaotisch und dazwischen periodisch. An den Verzweigungsstellen im Übergangsbereich findet jeweils eine Periodenverdopplung statt.

Bei Übergang von periodischen Verhalten zum Chaos kann ein typisches Phänomen auftreten, das als Periodenverdopplung oder Feigenbaum-Szenario bezeichnet wird. Dabei nimmt zum chaotischen Bereich hin die Oszillationsperiode stufenweise um den Faktor zwei zu. Die zugehörigen Parameterintervalle werden mit zunehmender Periode immer kürzer. Das Verhältnis der Längen aufeinander folgender Parameterintervalle unterschiedlicher Perioden strebt dabei gegen die Feigenbaum-Konstante δ≈4,669, eine irrationale Zahl. Dabei ist der chaotische Bereich oft auf fraktale Weise immer wieder von Intervallen mit periodischem Verhalten durchbrochen, die jeweils wiederum über Periodenverdopplung in das benachbarte Chaos übergehen. Dieses Verhalten und das zugehörigen Zahlenverhältnis hängen nicht von den Details des mathematischen oder physikalischen nichtlinearen Systems ab, sondern stellen ein universelles und damit fundamentales Gesetz vieler chaotischer Systeme dar.

Ein einfaches Beispiel ist ein tropfender Wasserhahn, betrachtet als diskretes System der aufeinanderfolgenden Zeitabstände zwischen zwei Tropfen. Die Stellung des Hahns ist dabei der Kontrollparameter. Bei hinreichend kleinem Leck fallen die Tropfen in regelmäßigen Abständen. Bei hinreichend großem dagegen ist keine Periodizität erkennbar, sondern die Folge der Zeitabstände ist chaotisch. Bei einer bestimmten Hahnstellung dazwischen lassen sich zwei verschiedene Zeitabstände beobachten, die abwechselnd aufeinanderfolgen. Das System befindet sich nicht nach jedem Tropfen wieder im selben Zustand sondern erst nach jedem zweiten. Eine solche Hahnstellung ist in der Praxis jedoch nur schwer zu finden.

Intermittenz

Neben der Periodenverdopplung werden auch andere Formen des Übergangs ins Chaos beobachtet, wie beispielsweise die sogenannte Intermittenz. Dabei wechseln sich bei einem Parameterwert im Übergangsbereich quasiperiodisches und chaotisches Verhalten ständig ab, wobei zu chaotischen Parameterwerten hin der chaotische Anteil ständig zunimmt.

Beispiele für chaotische Systeme

Den meisten Vorgängen in der Natur liegen nichtlineare Prozesse zugrunde. Entsprechend vielfältig sind die Systeme, die chaotisches Verhalten zeigen können. Hier einige wichtige oder bekannte Beispiele:

  • Das Wetter. Zur Zeit ist die Zuverlässigkeit der Wettervorhersage durch die grobe Kenntnis des Ausgangszustandes begrenzt. Aber auch bei vollständiger Information würde eine langfristige Wettervorhersage letztlich am chaotischen Charakter des meteorologischen Geschehens scheitern. Die Stabilität des Wetters kann stark schwanken. So sind bei bestimmten Wetterlagen Vorhersagen für eine Woche durchaus möglich, bei anderen dagegen kaum für 24 Stunden.
  • Das Doppelpendel. Da es sich aufgrund von nur zwei unabhängigen Freiheitsgraden leicht modellieren und auch leicht herstellen lässt, ist es ein beliebtes Demonstrationsobjekt für überraschende Wechsel im chaotischen Bewegungsablauf. In Computersimulationen und bei den Versuchen lassen sich bestimmte Klassen von Systemverhalten identifizieren, wie beispielsweise die maximal mögliche Anzahl von Überschlägen in Abhängigkeit von der anfänglichen Energie und der Reibung.
  • Das magnetische Pendel, bei dem eine an einem Faden aufgehängte Eisenkugel über mehreren Magneten pendelt.
  • Systeme mit stoßenden Kugeln. Wichtig ist, dass die Kugeln entweder kollidieren oder an gekrümmten Hindernissen reflektiert werden, damit Störungen exponentiell anwachsen. Beispiele sind das Gerät zur Ziehung der Lottozahlen, der Flipperautomat und Billard.
  • Das Dreikörperproblem und damit auch Sternsysteme aus drei oder mehr Sternen wie beispielsweise Sternhaufen.
  • Der Herzrhythmus. Je nach Gesundheitszustand lässt sich der Herzrythmus über chaostheoretische Kriterien klassifizieren. Auf diese Weise ist es möglich, bei Herzinfarktpatienten durch statistische Analysen des EKG eine Aussage über das Rückfallrisiko zu treffen. Ferner haben chaostheoretische Untersuchungen zu Herzschrittmachern ergeben, dass streng periodische Impulse weniger günstig sind als nur ungefähr periodische, was auch dem natürliche Schlagrhythmus des Herzens entspricht. Aus ähnlichen Gründen halten Motoren länger, wenn die Zahnräder nicht perfekt sind, so dass sich die Zähne nicht immer an der selben Stelle berühren.
  • Turbulenz wie beispielsweise beim Bénard-Experiment zur Konvektion.
  • Die Belousov-Zhabotinsky-Reaktion, eine chemische Reaktion.
  • Die Populationsdynamik in Räuber-Beute-Modellen.
  • Die Bäcker-Transformation, ein diskretes System, das den Ort einer Rosine im Kuchenteig beim abwechselnden Auswalzen und Falten des Teigs betrachtet.
  • Börsenkurse.

Geschichte

Ende des 19. Jahrhunderts gewann Henri Poincaré einen Preis mit dem Lösungsansatz für die Frage, ob das Sonnensystem stabil ist. Manche Quellen geben dies als die Geburtsstunde der Chaosforschung an, es dauerte jedoch bis in die Mitte des 20.Jahrhunderts bis der Lösungsansatz von Poincaré mit Hilfe von Computern brauchbar umgesetzt werden konnte.

Chaotische Phänomene sind schon seit langem bekannt, wie beispielsweise das Dreikörperproblem oder Turbulenz. Lange Zeit wurden diese Phänomene als eher weniger verbreitete Spezialfälle angesehen. Da eine angemessene Untersuchung ohne Computer wenig erfolgversprechend schien, und kaum jemand besondere Erkenntnisse erwartete, da die Phänomene vollständig auf den Konzepten der klassischen Physik beruhen, wurden sie wenig beachtet. Das änderte sich erst mit dem Aufkommen schneller Computer.

In den 1960er Jahren entdeckte Edward N. Lorenz die Phänomene, die heute als deterministisches Chaos bezeichnet werden, an einem Modell für das Wetter mit einem Gleichungssatz von drei Gleichungen zur Strömungsmechanik. Als er, um Zeit zu sparen, gerundete Werte einer früheren Berechnung verwendete, beobachtete er, dass winzige Änderungen der Anfangsbedingen nach kurzer Zeit zu völlig unterschiedlichen Ergebnissen führten. Der daraus abgeleitete Schmetterlingseffekt und die Formulierung des Begriffs der sensitiven Abhängigkeit von Anfangsbedingungen wurden zu häufig missgedeuteten Metaphern der „Chaostheorie“.

In den 1970 - 80er Jahren entdeckte Mitchell Feigenbaum die Phänomene der logistischen Gleichung und die nach ihm benannte Feigenbaum-Konstante. Diese Gleichung korrespondiert mit der von Benoit Mandelbrot 1980 untersuchten Mandelbrot-Menge, da sie ebenfalls auf einer quadratischen Gleichung beruht.

Etwa zur selben Zeit arbeiteten Siegfried Großmann in Marburg und Hermann Haken in Stuttgart an der Formulierung ihrer Theorien, die bald von den Ideen um Mandelbrot und Feigenbaum inspirieren wurden. Großmann formulierte eine Beschreibung des Lasers mit Hilfe der nichtlinearer Dynamik, und Haken gilt als Begründer der Synergetik und Entdecker des sogenannten Versklavungseffekts.

Die Mandelbrot-Menge, populär "Apfelmännchen" genannt, gilt als eins der formenreichsten Fraktale, das überhaupt bekannt ist. Entsprechende farbige Darstellungen in den Medien erregten Ende der 1980er Jahre Aufsehen in der Öffentlichkeit. Durch diese Bilder und die vermutete Nähe der Chaosforschung zu scheinbar unverstandenen Phänomenen des Alltags entwickelte sich in dieser Zeit ein großes Interesse der Öffentlichkeit an diesem Thema. Dabei entstanden überzogene Erwartungen, die die Chaosforschung nicht erfüllen konnte. Hinsichtlich der oft als neu und wesentlich für die Chaosforschung angesehene Aufgabe der Vorhersagbarkeit wurde meist übersehen, dass in der Physik bereits seit der Entwicklung der Quantentheorie in den 1920er Jahren der Determinismus kein grundlegendes Prinzip der Beschreibung der Natur mehr darstellt.

Ende der 1980er Jahre postulierte James Gleick in dem Buch „Chaos: making a new science“ einen Paradigmenwechsel in der Physik. Er bezog sich auf eine Abkehr von der Vorstellung einer besseren Beherrschbarkeit technischer Prozesse durch immer bessere Mess- und Berechnungsmethoden sowie von Großexperimenten hin zu kleinen Versuchsaufbauten, wie dem Doppelpendel oder dem tropfenden Wasserhahn, und zugehörigen Computerexperimenten.

Dieses Buch wurde sehr populär und trug mit zu einem Hype der Chaosforschung bei. In den Medien wurde intensiv, aber mehr oder weniger seriös „Chaostheorie“ oder Chaosforschung thematisiert. An vielen Universitäten wurden Arbeitsgruppen eingerichtet, wie z.B. in Graz, Wien oder Regensburg. In München wirkte die „Chaosgruppe der TU München“ mit zahlreichen Forschungsprojekten am Lehrstuhl für Didaktik der Physik. Sie wurde später in einen Forschungsverein umgewandelt. Sie veranstaltete eine Ringvorlesung und mehrere Jahrestagungen, bei denen versucht wurde, die gesamte Bandbreite der Chaosforschung zu repräsentieren und einen interdisziplinären Dialog zu ermöglichen. Es entstanden auch große Forschungsinstitute wie z. B. das Santa Fe Institut (USA) oder das Institut für nichtlineare Dynamik in Potsdam.

Mitte der 1990er Jahre ließ das Interesse der Öffentlichkeit an dem Thema Chaos nach. So wurde der Chaosforschung vorgeworfen, durch eine übermäßige interdisziplinäre Orientierung zu beliebig geworden zu sein. Auch ist es bis heute nicht gelungen, die Chaosforschung als eigenständige Disziplin zu etablieren, und eine einheitliche Chaostheorie zu formulieren. Gleichzeitig ging die Sturm-und-Drang-Zeit der Chaosforschung zu Ende, und die Forschungen zog sich zunehmend wieder in die einzelnen Disziplinen zurück, wie z. B. Turbulenzforschung, Wetterforschung, Medizinforschung und natürlich auch Mathematik und Physik. Die aktuelle Forschung befasst sich eher mit einem uneinheitlichen Satz von Phänomenen und Theorien. Viele Forscher, die sich heute noch mit der Thematik beschäftigen, würden sich nicht mehr als Chaosforscher bezeichnen.

Siehe auch

Chris Langtons Ameise (Turingmaschine), Systemtheorie, Volterra-Gesetze, Bifurkation, Komplexe Systeme, fraktale Geometrie

Literatur

Weblinks

Quelle: https://de.wikipedia.org/wiki/Spezial:Permanenter_Link/12591944