„SEIR-Modell“ – Versionsunterschied

Als SEIR-Modell bezeichnet man in der mathematischen Epidemiologie einen Ansatz zur Beschreibung der Ausbreitung von ansteckenden Krankheiten. Die Beschreibung ist näher am realen Verlauf als die des SIR-Modells, da hier berücksichtigt wird, dass ein Individuum nach seiner Infektion nicht sofort selbst infektiös ist. Im Gegensatz zu einem Individuums-basierten Modell (IBM) ist die Beschreibung makroskopisch, d. h. die Population wird als Gesamtheit betrachtet.

Gleichungssystem

Die Population von N Individuen sei zerlegt in die vier Kompartimente S, E, I, R, so dass

S+E+I+R=1.

bzw.

NS+NE+NI+NR=N.

Jedes Individuum kann die Prozedur

Susceptible (S) → Exposed (E) → Infectious (I) → Recovered (R)

durchlaufen. Die Ausbreitungsdynamik der Krankheit wird beschrieben durch

{\begin{aligned}S'&=-\beta SI,\\E'&=\beta SI-aE,\\I'&=aE-\gamma I,\\R'&=\gamma I.\end{aligned}}

Es handelt sich hierbei um ein nichtlineares System von gewöhnlichen Differentialgleichungen.

Größe	Einheit	Erklärung
`S`(`t`)	1	Anteil der Anfälligen, engl. susceptible. Noch nicht infiziert.
`E`(`t`)	1	Anteil der Exponierten, engl. exposed. Infiziert, aber noch nicht infektiös.
`I`(`t`)	1	Anteil der Infektiösen, engl. infectious.
`R`(`t`)	1	Anteil der Erholten, engl. recovered oder resistant. Bzw. verstorben oder nach Symptomen in Quarantäne.
`t`	d	Zeit in Tagen, engl. time.
`β`	1/d	Transmissionsrate. Der Kehrwert ist die mittlere Zeit zwischen Kontakten.
`γ`	1/d	Gesundungsrate. Der Kehrwert ist die mittlere infektiöse Zeit.
`a`	1/d	Der Kehrwert ist die mittlere Latenzzeit.

Die mittlere Latenzzeit ist die durchschnittliche Zeit, die ein Individuum in der Gruppe E der Exponierten verbringt; diese ist zu unterscheiden von der mittleren Inkubationszeit, denn der Beginn der Infektiosität muss nicht mit dem Beginn der Symptome übereinstimmen.

Für die Transmissionsrate (Übertragungsrate) ist auch die Bezeichnung Kontaktrate geläufig. Eine genauere Überlegung zerlegt diese in ein Produkt $\beta =pc$ , wobei $p$ die Transmissionswahrscheinlichkeit und $c$ die eigentliche Kontaktrate ist.

Beziehung zur Basisreproduktionszahl

Es lässt sich eine Beziehung zur Basisreproduktionszahl herstellen. Damit sich die Krankheit nicht weiter ausbreitet, muss $E'=0$ und $I'=0$ sein. Einsetzung dieser Bedingungen in die Differentialgleichungen führt zu $aE=\beta SI$ und $aE=\gamma I$ , und somit $\beta S=\gamma$ . Man betrachte nun außerdem die Gleichung $R_{q}:=R_{0}S$ bzw. $R_{q}:=(1-q)R_{0}$ mit $q:=1-S$ . Hierbei ist $R_{q}$ die Netto- und $R_{0}$ die Basisreproduktionszahl. Da die Bedingung $I'=0$ mit $R_{q}=1$ gleichbedeutend ist, ergibt sich

\beta =R_{0}\gamma .

Alternativ kann man sich überlegen, dass wenn ein Individuum im Mittel $\beta$ Kontakte pro Zeiteinheit hat, es über die mittlere infektiöse Zeit $\gamma ^{-1}$ dann $\beta \gamma ^{-1}$ Kontakte bzw. neue Infektionen gegeben haben muss. D.h.

R_{0}=\beta /\gamma

.^[1]^[2]

Maximal möglicher Anteil an Infizierten

Die Basisreproduktionszahl bestimmt wesentlich den maximal möglichen Anteil von Infizierten an einer gegebenen Population. Bezeichnen wir die Gesamtanteil aller Infizierten mit $J$ , also $J(t)=E(t)+I(t)$ , so folgt aus dem obigen Differentialgleichungssystem

{\frac {\mathrm {d} J}{\mathrm {d} S}}={\frac {\mathrm {d} E+\mathrm {d} I}{\mathrm {d} S}}={\frac {-\gamma I+\beta SI}{-\beta SI}}={\frac {\gamma }{\beta S}}-1

,

oder mit der Basisreproduktionszahl $R_{0}={\frac {\beta }{\gamma }}$ einfach

{\frac {\mathrm {d} J}{\mathrm {d} S}}={\frac {1}{R_{0}S}}-1.

Mit Umstellung dieser Gleichung nach $\mathrm {d} J={\frac {\mathrm {d} S}{R_{0}S}}-\mathrm {d} S$ liefert eine Integration durch Trennung der Variablen

J(t)+S(t)-{\frac {1}{R_{0}}}\ln S(t)={\text{const}}

für alle t, wobei $\ln$ der natürliche Logarithmus ist. Insbesondere gilt damit

J(t)+S(t)-{\frac {1}{R_{0}}}\ln S(t)=J(0)+S(0)-{\frac {1}{R_{0}}}\ln S(0)

oder äquivalent

J(t)=J(0)+S(0)-{\frac {1}{R_{0}}}\ln S(0)+\underbrace {{\frac {1}{R_{0}}}\ln S(t)-S(t)} _{=:\ f(S(t))}.

Die Hilfsfunktion $f(x)=\ln {\frac {x}{R_{0}}}-x$ hat wegen $f'(x)={\frac {1}{R_{0}x}}-1$ ein Maximum bei $x={\frac {1}{R_{0}}}$ . Der maximal mögliche Anteil $J_{\max }$ der Infizierten wird also für $S(t)={\frac {1}{R_{0}}}$ erreicht, d. h. $J_{\max }$ hängt nur von der Basisreproduktionszahl und den Anfangswerten von $J$ und $S$ ab:

J_{\text{max}}=J(0)+S(0)-{\frac {1}{R_{0}}}\ln S(0)-{\frac {1}{R_{0}}}+{\frac {1}{R_{0}}}\ln {\frac {1}{R_{0}}}=J(0)+S(0)+{\frac {1}{R_{0}}}\left(\ln {\frac {1}{R_{0}S(0)}}-1\right).

Für eine neu auftretende Erkrankung wie eine Epidemie durch ein unbekanntes Virus gilt $S(0)=1$ und $J(0)=0$ , d. h. der maximal mögliche Anteil der Infizierten an der Population hängt in diesem Fall wie folgt von der Basisreproduktionszahl ab:

J_{\text{max}}=1+{\frac {1}{R_{0}}}\left(\ln {\frac {1}{R_{0}}}-1\right).

Diese Gleichung entspricht der unter SIR-Modell#Maximale Zahl der Infizierten angegebenen Gleichung für das SIR-Modell.

Anteil der Erholten am Ende der Epidemie

Im Zusammenhang mit der Basisreproduktionszahl steht auch, welcher Anteil der Population insgesamt infiziert wird, unter Annahme, die Epidemie würde ohne jegliche Quarantäne durchlaufen. Unter Heranziehung der Differentialgleichungen findet man

{\frac {\mathrm {d} S}{\mathrm {d} R}}={\frac {S'(t)}{R'(t)}}=-{\frac {\beta S}{\gamma }}=-R_{0}S.

Für den Anfangswert $R(0)=0$ ist demnach

S(t)=S(0){\mathrm {e} }^{-R_{0}R(t)}.

Bei $t\to \infty$ ist nun $E=I=0$ , und daher $S+R=1$ . Daraus resultiert die Gleichung

1-q=S(0){\mathrm {e} }^{-R_{0}q},\quad q:=\lim _{t\to \infty }R(t).

Algebraische Umformung führt zur Gleichung

-R_{q}{\mathrm {e} }^{-R_{q}}=(q-1)R_{0}{\mathrm {e} }^{(q-1)R_{0}}=-S(0)R_{0}{\mathrm {e} }^{-R_{0}}.

Mit $x:=-S(0)R_{0}\mathrm {e} ^{-R_{0}}$ und $y:=(q-1)R_{0}$ lautet die letzte Gleichung $y\mathrm {e} ^{y}=x$ , die mit der lambertschen W-Funktion $W(x)$ nach $y$ umgestellt werden kann, d. h. $y=W(x)$ , was wieder zurückersetzt und nach $q$ umgestellt

q=1+{\frac {1}{R_{0}}}W(-S(0)R_{0}{\mathrm {e} }^{-R_{0}})

ergibt.

Für die praktische Berechnung des hier relevanten Teils der W-Funktion betrachtet man das quadratische Taylorpolynom der Funktion $f(w):=w\mathrm {e} ^{w}-x$ an der Stelle −1 und bestimmt von diesem die Nullstelle, auf welche noch einmalig die Fixpunktiteration $w\mapsto x\mathrm {e} ^{-w}$ angewendet wird. Das Resultat ist

w=x\exp(1-{\sqrt {2\mathrm {e} x+2}}).

Eine gute Näherung der W-Funktion erhält man nun als

W(x)\approx \varphi ^{n}(w),

wobei $\varphi ^{n}$ die n-te Iteration des Newtonverfahrens

\varphi (w)=w-{\frac {f(w)}{f'(w)}}={\frac {x\mathrm {e} ^{-w}+w^{2}}{w+1}}

ist. Für alle praktischen Bedürfnisse ist $n=4$ völlig ausreichend.

Exponentielle Anfangsphase

Am Anfang der Epidemie verläuft die Ausbreitung der Krankheit in guter Näherung exponentiell. Mit dem Ansatz $I=I(0){\mathrm {e} }^{\lambda t}$ kommt die Beziehung $I'=\lambda I$ hinzu. Hiermit gilt nun $aE=\gamma I+\lambda I$ und $R=\gamma I/\lambda$ . Infolge gilt

1-S=E+I+R={\frac {\gamma +\lambda }{a}}I+I+{\frac {\gamma }{\lambda }}I={\Big (}{\frac {\gamma +\lambda }{a}}+1+{\frac {\gamma }{\lambda }}{\Big )}I.

Leitet man diese Gleichung nun auf beiden Seiten ab, benutzt $-S'=\beta SI$ und dividiert anschließend durch $I$ , bekommt man

\beta S={\Big (}{\frac {\gamma +\lambda }{a}}+1+{\frac {\gamma }{\lambda }}{\Big )}\lambda

bzw.

a\beta S=(\lambda +a)(\lambda +\gamma ).

Da am Anfang in sehr guter Näherung $S\approx 1$ ist, kann $S=1$ gesetzt werden, womit eine Beziehung zwischen den Parametern $a,\beta ,\gamma$ und der Wachstumskonstante $\lambda$ gewonnen ist.

Ein alternativer systematischer Ansatz betrachtet gleich $S=1$ , womit sich die Differentialgleichungen zu einem linearen System vereinfachen, das als

{\begin{pmatrix}E'\\I'\end{pmatrix}}={\begin{pmatrix}-a&\beta \\a&-\gamma \end{pmatrix}}{\begin{pmatrix}E\\I\end{pmatrix}}

beschrieben werden kann.^[3] Alle weiteren Betrachtungen sind damit überschattet durch die wohlbekannte Theorie der linearen Differentialgleichungen mit konstanten Koeffizienten und ihrer Eigenwerttheorie. Die Wachstumskonstante ist ein Eigenwert der Systemmatrix $J:={\big (}{\begin{smallmatrix}-a&\beta \\a&-\gamma \end{smallmatrix}}{\big )}$ , die bereits gefundene Gleichung bekommt man aus

\det(J-\lambda E_{2})=0.

Wie bei jedem exponentiellen Wachstumsvorgang ist die Wachstumskonstante $\lambda$ äquivalent zur anschaulicheren Vervielfachungszeit

T_{n}={\frac {\ln(n)}{\lambda }},

speziell zur Verdopplungszeit $T_{2}$ .

Beispielrechnung

Es folgt eine Beispielrechnung zu einer Parameterbelegung wie sie für die COVID-19-Pandemie 2020 in Deutschland abgeschätzt wurde.^[4] Die Ausbreitung verläuft bezüglich einer Basisreproduktionszahl von 2,4, was der Unterlassung wesentlicher Quarantäne entspricht. Zur numerischen Lösung des Anfangswertproblems genügt das Euler-Verfahren.

from numpy import array as vector

# Explizites Euler-Verfahren
def euler_method(f,t0,x0,t1,h):
    t = t0; x = x0
    a = [[t,x]]
    for k in range(0,1+int((t1-t0)/h)):
        t = t0 + k*h
        x = x + h*f(t,x)
        a.append([t,x])
    return a

def SEIR_model(beta,gamma,a):
    def f(t,x):
        S,E,I,R = x
        return vector([
            -beta*S*I,
            beta*S*I - a*E,
            a*E - gamma*I,
            gamma*I
        ])
    return f

def SEIR_simulation(beta,gamma,a,E0,I0,days,step=0.1):
    x0 = vector([1.0-E0-I0,E0,I0,0.0])
    return euler_method(SEIR_model(beta,gamma,a),0,x0,days,step)

def diagram(simulation):
    import matplotlib.pyplot as plot
    plot.style.use('fivethirtyeight')
    figure,axes = plot.subplots()
    figure.subplots_adjust(bottom = 0.15)
    axes.grid(linestyle = ':', linewidth = 2.0, color = "#808080")
    t,x = zip(*simulation())
    S,E,I,R = zip(*x)
    axes.plot(t,S, color = "#0000cc")
    axes.plot(t,E, color = "#ffb000", linestyle = '--')
    axes.plot(t,I, color = "#a00060")
    axes.plot(t,R, color = "#008000", linestyle = '--')
    plot.show()

def simulation1():
    N = 83200000 # Einwohnerzahl von Deutschland 2019/2020
    R0 = 2.4; gamma = 1/3.0
    return SEIR_simulation(
        beta = R0*gamma, gamma = gamma, a = 1/5.5,
        E0 = 40000.0/N, I0 = 10000.0/N, days = 140)

diagram(simulation1)

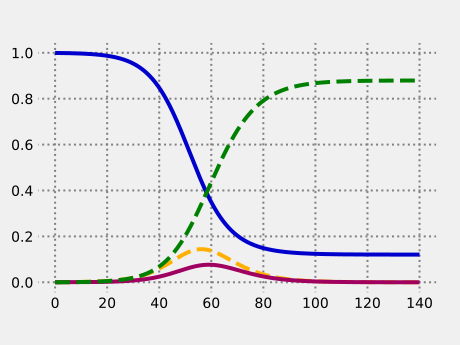Die vier Anteile, jeweils abhängig von der Zeit in Tagen. `S` in Blau, `E` in Gelb gestrichelt, `I` in Magenta, `R` in Grün gestrichelt.

Ersichtlich ist an diesem Beispiel, dass die Epidemie aufgrund der Aufheizung durch die Infektiösen auch noch nach dem Erreichen der kritischen Immunisierungsschwelle

q_{c}=1-{\frac {1}{R_{0}}}=58\,\%

weiterläuft. Insgesamt würden sich 88 % der Bevölkerung mit der Krankheit anstecken. Die Epidemie ließe sich allerdings spätestens nach Erreichen der kritischen Immunisierungsschwelle durch eine ca. einmonatige strenge Quarantäne stoppen.

Einbeziehung demografischer Dynamik

Unter der Annahme einer konstanten Sterberate $\mu$ und einer damit übereinstimmenden Geburtenrate wurde das erweiterte Modell

{\begin{aligned}S'&=\mu -\beta SI-\mu S,\\E'&=\beta SI-aE-\mu E,\\I'&=aE-\gamma I-\mu I,\\R'&=\gamma I-\mu R\end{aligned}}

formuliert. Gegenüber dem einfachen SEIR-Modell beschreibt dieses Modell auch einen langfristigen endemischen Verlauf, bei dem es zu einer Oszillation der Suszeptiblen $S$ kommen kann, bis sich $S$ ins durch

S'=E'=I'=R'=0

definierte Equilibrium eingependelt hat.

Für die Basisreproduktionszahl findet man hier bei Betrachtung des Equilibriums die Beziehung

R_{0}={\frac {\beta a}{(\mu +a)(\mu +\gamma )}}.

Zeitabhängige Transmissionsrate

Vorgänge wie Verhaltensänderungen, Quarantäne und Saisonalität bewirken eine Veränderung der Transmissionsrate. Diese Umstände finden ihre Berücksichtigung in der Modellierung der Transmissionsrate als zeitabhängige Funktion $\beta (t)$ , wobei das übrige Modell identisch beibehalten wird.^[5] Die einfachsten Ansätze für die Saisonalität nehmen die Transmissionsrate z. B. als Sinusschwingung an, mit Berg in den kälteren und Tal in den wärmeren Monaten.^[6]

Zu Bemerken ist, dass das Differentialgleichungssystem mit der expliziten Zeitabhängigkeit kein autonomes mehr ist und damit nicht mehr direkt ein dynamisches System vorliegt. Man kann aus dem System allerdings durch Hinzunahme der Gleichung $t'=1$ künstlich ein autonomes gewinnen.

Siehe auch

Mathematische Modellierung der Epidemiologie
SI-Modell (Ansteckung ohne Gesundung)
SIR-Modell (Ansteckung ohne Latenzzeit)
SIS-Modell (Ausbreitung von ansteckenden Krankheiten ohne Immunitätsbildung)

Literatur

Matt J. Keeling, Pejman Rohani: Modeling Infectious Diseases in Humans and Animals. Princeton University Press, 2008.
Matthias an der Heiden, Udo Buchholz: Modellierung von Beispielszenarien der SARS-CoV-2-Epidemie 2020 in Deutschland. Robert Koch-Institut, Abteilung für Infektionsepidemiologie (20. März 2020). DOI:10.25646/6571.2.

Einzelnachweise

↑ Institute for Desease Modeling: SEIR Model (abgerufen am 12.04.2020)
↑ C. Hubbs (2020): Social Distancing to Slow the Coronavirus (abgerufen am 12.04.2020)
↑ Junling Ma: Estimating epidemic exponential growth rate and basic reproduction number. In: Infectious Disease Modelling, Volume 5, 2020, S. 129–141, KeAi Publishing (17. Dez. 2019).
↑ Stellungnahme der Deutschen Gesellschaft für Epidemiologie (DGEpi) zur Verbreitung des neuen Coronavirus (SARS-CoV-2). (PDF) Deutsche Gesellschaft für Epidemiologie, 18. März 2020, abgerufen am 26. März 2020. Die der Beispielrechnung zugrunde liegende Version vom 19. März ist nicht mehr auffindbar. Hier ersatzweise die Version vom Vortag. Die aktuelle Version siehe hier.
↑ Gerardo Chowell, Cécile Viboud, Lone Simonsen, Seyed M. Moghadas: Characterizing the reproduction number of epidemics with early subexponential growth dynamics. In: J. R. Soc. Interface 13: 20160659 (17. August 2016). DOI: 10.1098/rsif.2016.0659.
↑ M. Keeling, P. Rohani: Modeling Infectious Diseases in Humans and Animals. Abschnitt 5.2. (S. 159): Modeling forcing in childhood infectious diseases: Measles.

[idm-seir-1] Institute for Desease Modeling: SEIR Model (abgerufen am 12.04.2020)

[2] C. Hubbs (2020): Social Distancing to Slow the Coronavirus (abgerufen am 12.04.2020)

[3] Junling Ma: Estimating epidemic exponential growth rate and basic reproduction number. In: Infectious Disease Modelling, Volume 5, 2020, S. 129–141, KeAi Publishing (17. Dez. 2019).

[dgepi-2020-03-19-4] Stellungnahme der Deutschen Gesellschaft für Epidemiologie (DGEpi) zur Verbreitung des neuen Coronavirus (SARS-CoV-2). (PDF) Deutsche Gesellschaft für Epidemiologie, 18. März 2020, abgerufen am 26. März 2020. Die der Beispielrechnung zugrunde liegende Version vom 19. März ist nicht mehr auffindbar. Hier ersatzweise die Version vom Vortag. Die aktuelle Version siehe hier.

[5] Gerardo Chowell, Cécile Viboud, Lone Simonsen, Seyed M. Moghadas: Characterizing the reproduction number of epidemics with early subexponential growth dynamics. In: J. R. Soc. Interface 13: 20160659 (17. August 2016). DOI: 10.1098/rsif.2016.0659.

[6] M. Keeling, P. Rohani: Modeling Infectious Diseases in Humans and Animals. Abschnitt 5.2. (S. 159): Modeling forcing in childhood infectious diseases: Measles.

[1]

[2]

[3]

[4]

[5]

[6]

@@ Zeile 64: / Zeile 64: @@
 Es lässt sich eine Beziehung zur [[Basisreproduktionszahl]] herstellen. Damit sich die Krankheit nicht weiter ausbreitet, muss <math>E'=0</math> und <math>I'=0</math> sein. Einsetzung dieser Bedingungen in die Differentialgleichungen führt zu <math>aE = \beta SI</math> und <math>aE=\gamma I</math>, und somit <math>\beta S = \gamma</math>. Man betrachte nun außerdem die Gleichung <math>R_q:=R_0 S</math> bzw. <math>R_q:=(1-q)R_0</math> mit <math>q:=1-S</math>. Hierbei ist <math>R_q</math> die Netto- und <math>R_0</math> die Basisreproduktionszahl. Da die Bedingung <math>I'=0</math> mit <math>R_q=1</math> gleichbedeutend ist, ergibt sich
 :<math>\beta = R_0\gamma.</math>
-Alternativ kann man sich überlegen, dass wenn ein Individuum im Mittel <math>\beta</math> Kontakte pro Zeiteinheit hat, es über die mittlere infektiöse Zeit <math>\gamma^{-1}</math> dann <math>\beta\gamma^{-1}</math> Kontakte bzw. neue Infektionen gegeben haben muss. D.h. <math>R_0 = \beta/\gamma</math>.
+Alternativ kann man sich überlegen, dass wenn ein Individuum im Mittel <math>\beta</math> Kontakte pro Zeiteinheit hat, es über die mittlere infektiöse Zeit <math>\gamma^{-1}</math> dann <math>\beta\gamma^{-1}</math> Kontakte bzw. neue Infektionen gegeben haben muss. D.h.
+:<math>R_0 = \beta/\gamma</math>.<ref name="idm-seir">Institute for Desease Modeling: [https://www.idmod.org/docs/hiv/model-seir.html SEIR Model] (abgerufen am 12.04.2020)</ref><ref>C. Hubbs (2020): [https://towardsdatascience.com/768292f04296 Social Distancing to Slow the Coronavirus] (abgerufen am 12.04.2020)</ref>
+== Maximal möglicher Anteil an Infizierten ==
+Die Basisreproduktionszahl bestimmt wesentlich den maximal möglichen Anteil von Infizierten an einer gegebenen Population. Bezeichnen wir die Gesamtanteil aller Infizierten mit <math>J</math>, also <math>J(t) = E(t) + I(t)</math>,
+so folgt aus dem obigen Differentialgleichungssystem
+:<math>
+\frac{\mathrm{d}J}{\mathrm{d}S}
+= \frac{\mathrm{d}E + \mathrm{d}I}{\mathrm{d}S}
+= \frac{-\gamma I + \beta SI}{-\beta SI}= \frac{\gamma}{\beta S} - 1
+</math>,
+oder mit der Basisreproduktionszahl <math>R_0 = \frac{\beta}{\gamma}</math> einfach
+:<math>
+\frac{\mathrm{d}J}{\mathrm{d}S} = \frac{1}{R_0 S} - 1.</math>
+Mit Umstellung dieser Gleichung nach <math>\mathrm{d}J = \frac{\mathrm{d}S}{R_0 S} - \mathrm{d}S</math> liefert eine Integration durch [[Trennung der Veränderlichen|Trennung der Variablen]]
+:<math>J(t) + S(t) - \frac{1}{R_0} \ln S(t) = \text{const}</math>
+für alle ''t'', wobei <math>\ln</math> der natürliche  [[Logarithmusfunktion|Logarithmus]] ist.
+Insbesondere gilt damit
+:<math>J(t) + S(t) - \frac{1}{R_0} \ln S(t) = J(0) + S(0) - \frac{1}{R_0} \ln S(0)</math>
+oder äquivalent
+:<math>J(t) = J(0) + S(0) - \frac{1}{R_0} \ln S(0) + \underbrace{\frac{1}{R_0} \ln S(t) - S(t)}_{=: \ f(S(t))}.</math>
+Die Hilfsfunktion <math>f(x) = \ln \frac{x}{R_0} - x</math> hat wegen <math>f'(x) = \frac{1}{R_0 x} - 1</math> ein Maximum bei <math>x = \frac{1}{R_0}</math>. Der maximal mögliche Anteil <math>J_{\max}</math> der Infizierten wird also für <math>S(t) = \frac{1}{R_0}</math> erreicht, d. h. <math>J_{\max}</math> hängt nur von der Basisreproduktionszahl und den Anfangswerten von <math>J</math> und <math>S</math> ab:
+:<math>
+J_{\text{max}}
+= J(0) + S(0) - \frac{1}{R_0} \ln S(0) -\frac{1}{R_0} + \frac{1}{R_0} \ln \frac{1}{R_0}
+= J(0) + S(0) + \frac{1}{R_0} \left( \ln \frac{1}{R_0 S(0)} - 1 \right).
+</math>
+Für eine neu auftretende Erkrankung wie eine Epidemie durch ein unbekanntes [[Virus]] gilt <math>S(0) = 1</math> und <math>J(0) = 0</math>, d. h. der maximal mögliche Anteil der Infizierten an der Population hängt in diesem Fall wie folgt von der Basisreproduktionszahl ab:
+:<math>
+J_{\text{max}}
+= 1 + \frac{1}{R_0} \left( \ln \frac{1}{R_0} - 1 \right).
+</math>
+Diese Gleichung entspricht der unter [[SIR-Modell#Maximale Zahl der Infizierten]] angegebenen Gleichung für das [[SIR-Modell]].
 == Anteil der Erholten am Ende der Epidemie ==

Deutschland Bundespräsident

„SEIR-Modell“ – Versionsunterschied

Version vom 12. April 2020, 10:37 Uhr

Inhaltsverzeichnis

Gleichungssystem

Beziehung zur Basisreproduktionszahl

Maximal möglicher Anteil an Infizierten

Anteil der Erholten am Ende der Epidemie

Exponentielle Anfangsphase

Beispielrechnung

Einbeziehung demografischer Dynamik

Zeitabhängige Transmissionsrate

Siehe auch

Literatur

Einzelnachweise

What are your Feelings

Wissen

Automated Chatbot

Data Security

Virtual Reality

Communication

Support

Über uns

Impressum

Datenschutz

Company

About Us

Services

Features

Our Pricing

Latest News

„SEIR-Modell“ – Versionsunterschied

Version vom 12. April 2020, 10:37 Uhr

Gleichungssystem

Beziehung zur Basisreproduktionszahl

Maximal möglicher Anteil an Infizierten

Anteil der Erholten am Ende der Epidemie

Exponentielle Anfangsphase

Beispielrechnung

Einbeziehung demografischer Dynamik

Zeitabhängige Transmissionsrate

Siehe auch

Literatur

Einzelnachweise

What are your Feelings

Share This Article :

Wissen

Automated Chatbot

Data Security

Virtual Reality

Communication

Support

Über uns

Impressum

Datenschutz

Company

About Us

Services

Features

Our Pricing

Latest News