Geometrische Reihe

Eine geometrische Reihe ist die Reihe $\textstyle \sum _{k=0}^{\infty }a_{k}$ einer geometrischen Folge $(a_{n})$ . Bei einer geometrischen Folge $(a_{n})$ ist der (formale) Quotient $q$ zweier benachbarter Folgenglieder konstant, es gilt also stets

a_{n+1}=a_{n}q

.

Explizit ausgedrückt gibt es also eine Konstante $c$ , sodass $a_{n}=cq^{n}$ für alle $n\geq 0$ . Das bedeutet, dass die Folgenglieder bezüglich des Summenindex einen exponentiellen Verlauf annehmen. Da der Fall $c=0$ trivial und in vielen Anwendungen auch nicht sinnvoll ist, und $c$ zugleich nur ein gemeinsamer Faktor aller Summanden der Reihe ist, wird in der Literatur meistens schlicht $c=1$ gesetzt. Die geometrische Reihe hat dann die vereinfachte Gestalt

1+q+q^{2}+q^{3}+q^{4}+\cdots

.

Aufgrund der einfachen Gestalt der Summanden ist es möglich die Partialsummen $\textstyle s_{n}:=\sum _{k=0}^{n}q^{k}$ der zugehörigen geometrischen Reihe explizit zu berechnen. Durch die Rekursion $s_{n}=s_{n-1}+q^{n}$ für $n\geq 0$ ergibt sich

s_{n}=1+q+q^{2}+\cdots +q^{n}=1+q(1+\cdots +q^{n-1})=1+qs_{n-1}=1+q(s_{n}-q^{n})

und durch Auflösen schließlich für $q\not =1$

s_{n}={\frac {1-q^{n+1}}{1-q}}

.

Eine wichtige Folgerung daraus ist, dass die geometrische Reihe $\textstyle \sum _{k=0}^{\infty }q^{k}$ genau dann konvergiert, falls $|q|<1$ gilt. Dabei ist es unerheblich, ob es sich bei $q$ um eine reelle oder allgemeiner komplexe Zahl handelt.

Die geometrische Reihe zählt zu den wichtigsten Reihen überhaupt. Anwendungen hat sie als Majorante (etwa beim Beweis von Konvergenzkriterien, wie dem Quotientenkriterium), im Bereich der Potenzreihenentwicklungen rationaler Funktionen und in der analytischen Kombinatorik.

Definition

Für reelle (oder komplexe) Zahlen $q$ definiert man die geometrische Reihe als^[1]

\sum _{n=0}^{\infty }q^{n}.

Ihre Partialsummen sind also gegeben durch $\textstyle s_{n}=\sum _{k=0}^{n}q^{k}$ , und die ersten Glieder sind

1,\quad 1+q,\quad 1+q+q^{2},\quad 1+q+q^{2}+q^{3},\quad \ldots .

In allgemeinerer Form wird für reelle (oder komplexe) Zahlen $a,q$ die Reihe

\sum _{n=0}^{\infty }aq^{n}=a+aq+aq^{2}+aq^{3}+\cdots =a\left(1+q+q^{2}+q^{3}+q^{4}+\cdots \right)

auch als geometrische Reihe bezeichnet. Diese ist jedoch bis auf einen skalaren Faktor gleich der geometrischen Reihe $\textstyle \sum _{n=0}^{\infty }q^{n}$ , weshalb meistens diese studiert wird.

Konvergenzkriterium

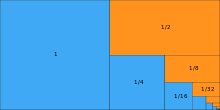
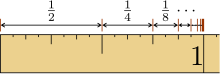
Für $|q|<1$ konvergiert die geometrische Reihe hingegen; es gilt in diesem Fall

\sum _{k=0}^{\infty }q^{k}=1+q+q^{2}+\dots ={\frac {1}{1-q}}

.

Bewiesen werden kann dies über Betrachtung der Partialsummen:

s_{n}:=\sum _{k=0}^{n}q^{k}={\frac {1-q^{n+1}}{1-q}}

,

und die letzte Gleichheit folgt aus

(1-q)s_{n}=\sum _{k=0}^{n}q^{k}-\sum _{k=1}^{n+1}q^{k}=1-q^{n+1}.

Es ist $q^{n}$ für $|q|<1$ eine Nullfolge, also gilt

\lim _{n\to \infty }s_{n}=\lim _{n\to \infty }{\frac {1-q^{n+1}}{1-q}}={\frac {1-0}{1-q}}={\frac {1}{1-q}}

.

Es ist also $|q|<1$ hinreichend für die Konvergenz der geometrischen Reihe. Zugleich ist dies jedoch auch notwendig: Für $|q|\geq 1$ folgt die Divergenz der Reihe $\textstyle \sum _{n=0}^{\infty }q^{n}$ aus dem Nullfolgenkriterium, da $q^{n}$ in diesem Fall für $n\to \infty$ nicht gegen 0 strebt.^[2]

Ein Quotient $q$ mit $|q|\geq 1$ ergibt eine divergente geometrische Reihe, z. B. für $q=2$ und Startwert $1$

1,~1+2,~1+2+4,~1+2+4+8,\dots

zusammengefasst also

1,~3,~7,~15,\dots

Im Falle der hier abgebildeten Zweierpotenzen erscheinen stets die Mersenneschen Zahlen $s_{n}=2^{n+1}-1$ als Werte der Summe.

Zahlenbeispiel

Gegeben sei die geometrische Folge

a_{0}=5,\ a_{1}=15,\ a_{2}=45,\ a_{3}=135,\ \dotsc

mit $a_{0}=5$ und $q=3.$ Die zugehörige geometrische Reihe ist

s=5\sum _{k=0}^{\infty }3^{k}=\sum _{k=0}^{\infty }5\cdot 3^{k}=5+15+45+135+\dotsb =\infty .

Die zugehörige Folge von Partialsummen ergibt sich zu

s_{0}=5=5{\frac {1-3^{1}}{1-3}}

s_{1}=5+15=20=5{\frac {1-3^{2}}{1-3}}

s_{2}=5+15+45=65=5{\frac {1-3^{3}}{1-3}}

s_{3}=5+15+45+135=200=5{\frac {1-3^{4}}{1-3}}

usw.

Geometrische Veranschaulichungen

Zur Summenformel

Das große gleichseitige Dreieck $ABC$ , dessen Flächeninhalt ohne Beschränkung der Allgemeinheit als $1$ angenommen wird, setzt sich aus drei flächengleichen unendlichen Folgen gleichseitiger Dreiecke (rot, gelb, blau) zusammen, deren Grenzwerte jeweils ${\tfrac {1}{3}}$ mal so groß sind wie das Dreieck $ABC$ (Figur 1). Wegen der Selbstähnlichkeit der Dreiecke $ABC$ , $A_{1}B_{1}C$ , $A_{2}B_{2}C$ , … und ihrer Mittendreieck-Eigenschaften besitzt jede der drei Dreiecksfolgen den Grenzwert

\sum _{k=1}^{\infty }\left({\frac {1}{4}}\right)^{k}

.

Also gilt^[3]^[4]

\sum _{k=1}^{\infty }\left({\frac {1}{4}}\right)^{k}={\frac {1}{3}}

.

Zu einer verwandten Summenformel

In Figur 2 gilt:

1+2\cdot {\frac {1}{2}}+3\cdot {\frac {1}{4}}+4\cdot {\frac {1}{8}}+5\cdot {\frac {1}{16}}+\ldots =4

.

Dies bestätigt die Partialsummenformel

s_{n}=a_{0}\sum _{k=0}^{n}q^{k}k

für $a_{0}=2$ , $q={\tfrac {1}{2}}$ und $n=5$ .^[5]^[6]

Geschichte

Bei Zenon von Elea

Im antiken Griechenland beschäftigte sich Zenon von Elea (ca. 490 v. Chr. bis 430 v. Chr.) bereits mit Paradoxien und Trugschlüssen, die beim Umgang mit dem Unendlichen entstehen können. Oft handelte es sich dabei um Gedankenexperimente im Umfeld von Raum, Zeit und Bewegung.

Teilungsparadoxon

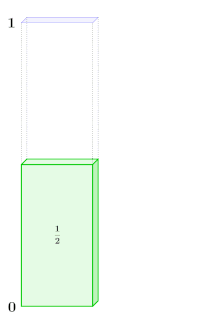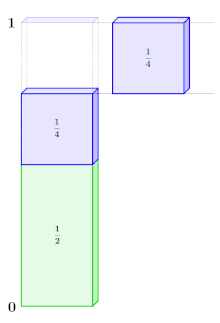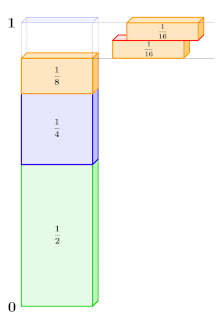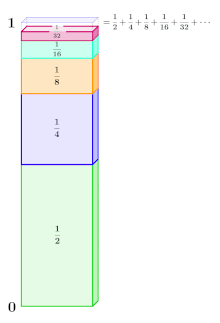
Bereits vor ca. 2500 Jahren standen griechische Mathematiker vor einem Paradoxon, das beim Gehen von einem Ort zum anderen entstehen kann: Sie glaubten, dass stets eine unendlich lange Liste von Zahlen, die alle größer als null sind, zu unendlich summiert wird. Deshalb erschien es paradox, als Zenon von Elea im Rahmen seines Teilungsparadoxons darauf hinwies, dass man, um von einem Ort zum anderen zu gelangen, zuerst die Hälfte der Strecke gehen muss, dann die Hälfte der verbleibenden Strecke und danach wieder die Hälfte der dann noch verbleibenden Strecke. Dieser Vorgang setzt sich unendlich oft fort, da man, egal wie klein die verbleibende Strecke ist, immer die erste Hälfte davon zurücklegen muss. Dadurch verwandelte Zenon von Elea eine kurze Strecke in eine unendlich lange Liste von halbierten Reststrecken, die allesamt größer als null sind. Das Problem bestand nun darin: Wie kann eine Strecke beschränkt sein, da der Zielort offenbar niemals erreicht wird, und gleichzeitig unendlich lang, da man eine unendlich lange Liste positiver Strecken summiert? Das Paradoxon zeigte, dass die Annahme, eine unendlich lange Liste von Zahlen größer als null summiere sich zu unendlich, falsch war.

Achilles und die Schildkröte

Ein sehr anschauliches Beispiel für die Anwendung (und sogar Herleitung des Grenzwerts) der geometrischen Reihe ist Geschichte von Achilles und der Schildkröte.^[7]

Der für seine Schnelligkeit bekannte Athlet Achilles tritt in einem Wettlauf gegen eine langsame Schildkröte an. Beide starten zum selben Zeitpunkt, aber die Schildkröte erhält anfangs einen Vorsprung von, zum Beispiel $100\,{\text{m}}$ . Obwohl Achilles mit einer um den Faktor $p$ , mit $p>1$ , höheren Geschwindigkeit als die der Schildkröte läuft, kann er sie scheinbar niemals einholen. Denn: Sobald Achilles $100\,{\text{m}}$ weit gelaufen ist, also den Punkt erreicht hat, an dem die Schildkröte gestartet ist, ist eine gewisse Zeit verstrichen. In dieser Zeit hat die Schildkröte die Strecke $100\,{\text{m}}/p$ zurückgelegt. Achilles muss also die entsprechende Strecke weiterlaufen, um die Schildkröte einzuholen. Derweil hat die Schildkröte jedoch weitere $100\,{\text{m}}/p^{2}$ zurückgelegt. Achilles hat die Schildkröte immer noch nicht eingeholt. Er läuft entsprechend weiter, muss nun allerdings feststellen, dass die Schildkröte in der Zwischenzeit abermals eine gewisse Strecke zusätzlich zurückgelegt hat; dieses Mal sind es $100\,{\text{m}}/p^{3}$ . Dieses Spiel setzt sich unendlich oft fort.

Der Punkt $x$ , an welchem Achilles die Schildkröte endlich einholen wird, ist gegeben durch die unendliche Summe

x=100\,{\text{m}}+{\frac {100\,{\text{m}}}{p}}+{\frac {100\,{\text{m}}}{p^{2}}}+{\frac {100\,{\text{m}}}{p^{3}}}+\dots =100\,{\text{m}}\sum _{k=0}^{\infty }p^{-k}.

Alternativ kann $x$ durch das Aufstellen zweier linearer Gleichungen bestimmt werden. Es seien

{\begin{aligned}x_{\text{S}}(t)&=v\,t+100\,{\text{m}}\quad {\text{bzw.}}\\x_{\text{A}}(t)&=p\,v\,t\end{aligned}}

die Bewegungsgleichungen der Schildkröte bzw. von Achilles, wobei $v$ die Geschwindigkeit der Schildkröte und $t$ die verstrichene Zeit ist. Es wird die $x$ -Koordinate des Schnittpunkts von $x_{\text{S}}(t)$ und $x_{\text{A}}(t)$ gesucht. Durch Gleichsetzen beider Gleichungen, Umformung auf $t$ und Einsetzen von $t$ in eine der beiden Gleichungen erhält man $x=100\,{\text{m}}/(1-1/p)$ . Der Wert ist endlich; Achilles wird die Schildkröte also doch einholen (womit sich das scheinbare Paradoxon auflöst). Wird diese Lösung mit derjenigen von oben verglichen, so findet man

{\begin{aligned}100\,{\text{m}}\sum _{k=0}^{\infty }p^{-k}={\frac {100\,{\text{m}}}{1-(1/p)}},\quad {\text{oder äquivalent}}\quad \sum _{k=0}^{\infty }q^{k}={\frac {1}{1-q}},\end{aligned}}

wobei im letzten Schritt auf beiden Seiten durch $100\,{\text{m}}$ geteilt und die Variable $q:=1/p$ , mit $0<q<1$ , eingeführt wurde.

Anwendungen

Rentenrechnung

Angenommen, man zahlt am Anfang eines jeden Jahres 2000 € bei einer Bank ein und die Zinsen liegen bei 5 % [d. h. der Zinsfaktor ist: $1+(5/100)=1{,}05$ ]. Wie viel Geld hat man am Ende des fünften Jahres?

Das im ersten Jahr eingezahlte Geld wird fünf Jahre lang verzinst, man erhält dafür am Ende inklusive Zinseszins $2000\cdot 1,05^{5}$ €. Das im zweiten Jahr eingezahlte Geld wird nur noch vier Jahre verzinst und so weiter. Insgesamt ergibt sich dann durch die Rentenrechnung nach fünf Jahren ein angesparter Betrag von

{\begin{aligned}&2\,000\cdot 1{,}05^{5}+2\,000\cdot 1{,}05^{4}+2\,000\cdot 1{,}05^{3}+2\,000\cdot 1{,}05^{2}+2\,000\cdot 1{,}05^{1}\\&\quad =2\,000\cdot 1{,}05\cdot (1{,}05^{4}+1{,}05^{3}+1{,}05^{2}+1{,}05^{1}+1{,}05^{0})\\&\quad =2\,000\cdot 1{,}05\cdot \sum _{k=0}^{4}1{,}05^{k}\\&\quad =2\,000\cdot 1{,}05\cdot {\frac {1{,}05^{4+1}-1}{1{,}05-1}}\\&\quad =11\,603{,}826\end{aligned}}

Durch Zinsen hat sich das Kapital somit um 1603,83 € erhöht. Beim Nachrechnen von Kontoauszügen ist zu bedenken, dass im Bankenwesen nicht mathematisch gerundet wird.

Zum Vergleich: Würden nicht Jahr für Jahr je 2000 € eingezahlt, sondern gleich von Beginn an die ganzen 10000 € über 5 Jahre bei 5 % Zinsen angelegt, so wäre der Endbetrag

10\,000\cdot 1{,}05^{5}=12\,762{,}8156

also ein Kapitalertrag von 2762,82 €.

Allgemein gilt: Beträgt die Einlage am Anfang jedes Jahres $a_{0}$ , der Zinsfaktor $q$ und die Laufzeit $n$ Jahre, dann ist der Endwert

a_{0}\sum _{k=1}^{n}q^{k}=a_{0}q{\frac {q^{n}-1}{q-1}}

.

Periodische Dezimalbrüche

Periodische Dezimalbruchentwicklungen enthalten eine geometrische Reihe, welche mit den obigen Formeln wieder in einen Bruch umgewandelt werden kann.^[8]

Beispiel 1:

{\begin{aligned}0{,}2{\overline {67}}&={\frac {2}{10}}+{\frac {67}{1000}}\cdot \sum _{k=0}^{\infty }\left({\frac {1}{100}}\right)^{k}={\frac {2}{10}}+{\frac {67}{1000}}\cdot {\frac {1}{1-{\frac {1}{100}}}}\\&={\frac {2}{10}}+{\frac {67}{1000}}\cdot {\frac {100}{99}}={\frac {2}{10}}+{\frac {67}{990}}={\frac {265}{990}}={\frac {53}{198}}.\end{aligned}}

Beispiel 2:

0{,}{\overline {9}}={\frac {9}{10}}+{\frac {9}{100}}+{\frac {9}{1000}}+\dotsb ={\frac {9}{10}}\cdot \sum _{k=0}^{\infty }\left({\frac {1}{10}}\right)^{k}={\frac {9}{10}}\cdot {\frac {1}{1-{\frac {1}{10}}}}={\frac {9}{10}}\cdot {\frac {10}{9}}=1.

Verallgemeinern lässt sich dies auf sog. g-ale Entwicklungen: Ist eine ganze Zahl $g\geq 2$ fest gewählt, und $x_{k}\in \{0,\ldots g-1\}$ eine Folge, so heißt

x=\sum _{k=1}^{\infty }x_{k}g^{-k}

die g-ale Entwicklung der reellen Zahl $x$ . Wegen der Abschätzung,

0\leq \sum _{k=1}^{\infty }x_{k}g^{-k}\leq (g-1)\sum _{k=1}^{\infty }g^{-k}=1

welche die geometrische Reihe nutzt, gilt zudem $x\in [0,1]$ .^[9] Dies kann dazu verwendet werden, die Überabzählbarkeit der reellen Zahlen zu zeigen.^[10]

Wahrscheinlichkeitstheorie

Geometrische Verteilung

Wahrscheinlichkeiten sind Konzepte der Maßtheorie und können damit als „Teilvolumina“ des „Ganzen mit Volumen Eins“ gesehen werden.^[11] Sie messen Plausibilität. Das Quadrat mit Fläche = 1 repräsentiert „alles, was möglich ist“. Bildlich wird die Unterteilung der verschiedenen Ausgänge des Spiels gezeigt. Die Flächen korrespondieren zu den Summanden der normalisierten geometrischen Reihe $\textstyle \sum _{k=0}^{\infty }r(1-r)^{k}=1$ ( $0<r<1$ ), und die Plausibilität nimmt ab.

Die geometrische Reihe kommt bei der namensverwandten geometrischen Verteilung zum Einsatz.^[12] Diese modelliert ein beliebig häufig wiederholtes Bernoulli-Experiment mit möglichen Ausgängen

„Erfolg“ mit Wahrscheinlichkeit $r$
„Misserfolg“ mit Wahrscheinlichkeit $1-r$ .

In einem Spiel wird Runde für Runde so lange gespielt, bis ein Erfolg vorliegt (womit das Spiel endet). Liegt sofort ein Erfolg vor, korrespondiert dies zu der Wahrscheinlichkeit $r$ , bei einem Misserfolg und einem anschließenden Erfolg ist es $(1-r)r$ . Allgemein bezieht sich $(1-r)^{n}r$ auf $n$ Misserfolge hintereinander mit einem anschließenden Erfolg in der $n+1$ -ten Runde. Bei positiver Erfolgswahrscheinlichkeit $r>0$ wird fast sicher irgendwann mal ein Erfolg eintreffen; gleichzeitig repräsentieren die $r^{n}(1-r)$ alle unterschiedliche Ereignisse. Damit erhält die geometrische Reihe eine probabilistische Interpretation:

r+(1-r)r+(1-r)^{2}r+(1-r)^{3}r+(1-r)^{4}r+\cdots =1.

Ruin des Spielers

Die geometrische Reihe spielt auch beim sog. Ruin des Spielers eine zentrale Rolle. Ausgangspunkt ist ein Spiel zwischen einem Spieler und der Bank, das in mehreren Runden ausgetragen wird. Jede Runde läuft unabhängig von der vorherigen ab, und mit Wahrscheinlichkeit $p$ gewinnt der Spieler einen Euro in einer Runde. Entsprechend verliert der Spieler mit der Gegenwahrscheinlichkeit $q=1-p$ einen Euro in einer Runde gegen die Bank. Angenommen wird, dass der Spieler mit einem Kapital von $i$ Euro startet und die Bank $a-i>0$ an Kapital besitzt. Die Frage ist, mit welcher Wahrscheinlichkeit $q_{i}$ der Spieler verlieren wird, also sein Kapital komplett verbraucht (die Bank verliert, wenn der Spieler irgendwann $a$ Euro besitzt, ohne davor pleitegegangen zu sein).^[13] Über die geometrische Reihe kann man diese Wahrscheinlichkeit in Abhängigkeit von $p$ , $a$ und $i$ ausdrücken:^[14]

q_{i}=1-{\frac {({\frac {p}{q}})^{a-i}-({\frac {p}{q}})^{a}}{1-({\frac {p}{q}})^{a}}}.

Fraktale Geometrie

Die Fläche innerhalb der Kochschen Schneeflocke kann als Vereinigung von unendlich vielen gleichseitigen Dreiecken beschrieben werden (siehe Abbildung). Jede Seite des grünen Dreiecks ist genau ${\tfrac {1}{3}}$ so groß wie eine Seite des großen blauen Dreiecks und hat daher genau ${\tfrac {1}{9}}$ der Fläche. Ebenso hat jedes gelbe Dreieck ${\tfrac {1}{9}}$ der Fläche eines grünen Dreiecks, und so weiter. Wenn man das blaue Dreieck als Einheit der Fläche nimmt, ergibt die gesamte Fläche der Schneeflocke

1+3\left({\frac {1}{9}}\right)+12\left({\frac {1}{9}}\right)^{2}+48\left({\frac {1}{9}}\right)^{3}+\cdots .

Der erste Term dieser Reihe repräsentiert die Fläche des blauen Dreiecks, der zweite Term die Gesamtfläche der drei grünen Dreiecke, der dritte Term die Gesamtfläche der zwölf gelben Dreiecke, und so weiter. Abgesehen von der anfänglichen 1 ist diese Reihe geometrisch mit einem konstanten Verhältnis $r={\tfrac {4}{9}}$ . Der erste Term der geometrischen Reihe ist $a=3\cdot {\tfrac {1}{9}}={\tfrac {1}{3}}$ , sodass die Summe

1+{\frac {a}{1-r}}=1+{\frac {\frac {1}{3}}{1-{\frac {4}{9}}}}={\frac {8}{5}}

ist. Somit ist die Fläche der Kochschen Schneeflocke Faktor ${\tfrac {8}{5}}$ der Fläche des Basisdreiecks.

Harmonische Reihe

Die $n$ -te harmonische Zahl ist gegeben durch

H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots +{\frac {1}{n}}.

Über die geometrische Reihe erhält man die Integralformel

H_{n}=\int _{0}^{1}{\frac {1-t^{n}}{1-t}}\mathrm {d} t.

Damit kann eine Verallgemeinerung definiert werden: Für komplexe Werte $s$ mit $\mathrm {Re} (s)>-1$ kann man

H_{s}=\int _{0}^{1}{\frac {1-t^{s}}{1-t}}\mathrm {d} t

definieren, und es gilt

H_{s-1}+{\frac {1}{s}}=H_{s}.

Funktionentheorie

Als Majorante

In der Theorie der Potenzreihen nimmt die geometrische Reihe die Rolle einer Majorante ein. Grob gesagt ist die Idee, eine allgemeine Potenzreihe $\textstyle \sum _{n=0}^{\infty }a_{n}q^{n}$ durch die geometrische Reihe $\textstyle \sum _{n=0}^{\infty }q^{n}$ zu „imitieren“. Eine wichtige Aussage in diesem Kontext ist die Existenz eines Konvergenzradius für Potenzreihen: Für jede formale Potenzreihe $F(q)=\textstyle \sum _{n=0}^{\infty }a_{n}q^{n}$ existiert eine eindeutig bestimmte Zahl $0\leq R\leq \infty$ , so dass $F(q)$ für alle $|q|<R$ konvergiert und für alle $|q|>R$ divergiert. Dabei ist die Menge der $q$ mit $|q|<0$ bzw. $|q|>\infty$ per definitionem leer. Setzt man

R:=\sup\{\varrho \geq 0\colon (a_{n}\varrho ^{n})_{n\in \mathbb {N} _{0}}\quad {\text{ist Nullfolge}}\},

so existiert für alle $\varrho <\varrho _{1}<R$ eine Abschätzung für $|q|\leq \varrho$ :

|a_{n}q^{n}|\leq \left|a_{n}\varrho _{1}^{n}{\frac {\varrho ^{n}}{\varrho _{1}^{n}}}\right|\leq M_{\varrho _{1}}\cdot \left({\frac {\varrho }{\varrho _{1}}}\right)^{n}

für eine nur von $\varrho _{1}$ (und natürlich der Potenzreihe als ganze) abhängigen Konstanten $M_{\varrho _{1}}>0$ . Damit hat man

\sum _{n=0}^{\infty }|a_{n}q^{n}|\leq M\sum _{n=0}^{\infty }\left({\frac {\varrho }{\varrho _{1}}}\right)^{n}<\infty

also muss die Potenzreihe $\textstyle \sum _{n=0}^{\infty }a_{n}q^{n}$ in letzter Konsequenz für alle $|q|<R$ nach dem Majorantenkriterium konvergieren. Wegen des Nullfolgenkriteriums ist sie ferner nach Konstruktion für alle $|q|>R$ divergent. Damit zeigt sich, dass allgemeine Potenzreihen stets auf Kreisscheiben konvergieren, gerade weil die spezielle geometrische Reihe dies als Potenzreihe tut.^[15]

Explizite Taylor-Reihen

Taylor-Reihen zu einigen Funktionen können mittels der geometrischen Reihe berechnet werden. Das betrifft zum Beispiel die natürliche Logarithmusfunktion^[16]

-\log(1-x)=\int _{0}^{x}{\frac {\mathrm {d} t}{1-t}}=\int _{0}^{x}\sum _{n=0}^{\infty }t^{n}\mathrm {d} t=\sum _{n=0}^{\infty }{\frac {x^{n+1}}{n+1}}=x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}+{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}+\cdots ,\qquad (|x|<1).

Dabei wurde im letzten Schritt die Summe gliedweise integriert. Etwas ähnliches gilt auch für die Arkustangensfunktion:^[17]^[18]

\arctan(x)=\int _{0}^{x}{\frac {\mathrm {d} t}{1+t^{2}}}=\int _{0}^{x}\sum _{n=0}^{\infty }(-1)^{n}t^{2n}\mathrm {d} t=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n+1}}{2n+1}}=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+{\frac {x^{9}}{9}}-\cdots ,\qquad (|x|<1).

Ferner spielt die geometrische Reihe bzw. allgemein die Taylor-Reihen zu $z\mapsto (1-z)^{-m}$ um $z=0$ eine wichtige Rolle bei der Bestimmung der Taylor-Koeffizienten rationaler Funktionen.^[19] Hat die rationale Funktion

r(z)=\sum _{j=1}^{n}\sum _{h=1}^{m_{j}}{\frac {a_{j,h}}{(z-z_{j})^{h}}}

paarweise verschiedene Polstellen in $z_{1},\cdots ,z_{n}$ und strebt für $|z|\to \infty$ gegen 0, so ist ihre Taylor-Reihe um einen Punkt $z_{0}\notin \{z_{1},\ldots ,z_{n}\}$ stets von der Form^[20]

r(z)=\sum _{k=0}^{\infty }a_{k}(z-z_{0})^{k},

wobei

a_{k}=\sum _{j=1}^{n}p_{j}(k)(z_{j}-z_{0})^{-k},

mit den Polynomen

p_{j}(k)=\sum _{h=1}^{m_{j}}(-1)^{h}a_{j,h}{\frac {(z_{j}-z_{0})^{-h}}{(h-1)!}}(k+1)_{h-1}.

Dabei bezeichnet $(x)_{n}:=x(x-1)\cdots (x-n+1)$ die fallende Faktorielle. Es gilt auch die Umkehrung, d. h. Taylor-Koeffizienten dieser Art erzeugen rationale Funktionen.^[21] Unmittelbare Anwendung hat dieses sehr allgemeine Prinzip beim Auflösen von Differenzengleichungen.^[22] Ein Beispiel in diesem Kontext ist die explizite Formel von Binet für die Fibonacci-Folge $(f_{n})$ :^[23]

f_{n}={\frac {1}{\sqrt {5}}}\left(\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right).

Cauchyscher Entwicklungssatz

Ein zentrales Resultat der Funktionentheorie ist, dass holomorphe Funktionen analytisch sind. Das bedeutet, dass sie in jedem Punkt ihres (offenen) Definitionsbereichs in eine Potenzreihe entwickelt werden können, die in einer offenen Kreisscheibe konvergiert und dort die Funktion darstellt.^[24] Präziser gilt der Cauchysche Entwicklungssatz: Ist $c\in U$ mit offenem $U$ , $B_{r}(c)$ die größte Kreisscheibe um $c$ in $U$ und $f\colon U\to \mathbb {C}$ holomorph, so ist $f$ um $c$ in eine Taylorreihe $\textstyle \sum _{n=0}^{\infty }a_{n}(z-c)^{n}$ entwickelbar, die in $B_{r}(c)$ auf kompakten Teilmengen absolut und gleichmäßig konvergiert. Die Koeffizienten sind gegeben durch^[24]

a_{n}={\frac {f^{(n)}(c)}{n!}}={\frac {1}{2\pi i}}\oint _{\partial B_{d}(c)}{\frac {f(w)}{(w-c)^{n+1}}}\mathrm {d} w

, wobei

0<d<r.

Dabei wird der Integrationsweg in mathematisch positiver Richtung einfach durchlaufen (siehe auch komplexes Kurvenintegral). Bemerkenswert ist die Tatsache, dass für den Beweis des Entwicklungssatzes lediglich die Reihenentwicklungen der Funktionen $z\mapsto (z-c)^{-n-1}$ im Inneren des Integrals benötigt werden, was allgemein durch Ableitungen der geometrischen Reihe ausgedrückt werden kann, sowie Vertauschbarkeit von Summation und Integration. Für den Fall $k=0$ wurde dies bereits 1831 von Cauchy durchgeführt.^[25]

Abschätzung von Taylor-Koeffizienten

Das Wachstum der Taylor-Koeffizienten einer Potenzreihe sagt etwas über das Wachstum der zugehörigen Funktion aus, und umgekehrt. Um dies präziser zu fassen, ist es von Nutzen, die geometrische Reihe passend zu verallgemeinern. Mittels der Euler-Polynome $A_{m}(q)$ erhält man für ganze Zahlen $m\geq 0$

\sum _{n=1}^{\infty }n^{m}q^{n}={\frac {qA_{m}(q)}{(1-q)^{m+1}}}.

Dabei gilt stets $|A_{m}(q)|\leq m!$ für alle $|q|\leq 1$ . Gilt nun $|a_{n}|\leq Mn^{m}$ für die Koeffizienten einer Potenzreihe $\textstyle f(z):=\sum _{n=1}^{\infty }a_{n}q^{n}$ , so ist $f$ in der Einheitskreisscheibe $B_{1}(0)=\{z\in \mathbb {C} \colon |z|<1\}$ eine holomorphe Funktion, und es folgt

|f(q)|\leq \sum _{n=1}^{\infty }Mn^{m}|q|^{n}\leq {\frac {M|qA_{m}(q)|}{|1-|q||^{m+1}}}\leq {\frac {Mm!}{(1-|q|)^{m+1}}}.

In gewisser Weise kann diese Aussage umgekehrt werden. Mit Hilfe der Cauchyschen Integralformel folgt unter der Voraussetzung

|f(q)|\leq {\frac {M}{(1-|q|)^{m}}}

für ein $m\in \mathbb {N} _{0}$ und alle $|q|<1$ bereits für alle $0<r<1$ mit der Standardabschätzung für Integrale

|a_{n}|=\left|{\frac {1}{2\pi i}}\oint _{\partial B_{r}(0)}{\frac {f(q)}{q^{n+1}}}\mathrm {d} q\right|\leq {\frac {M}{2\pi }}{\frac {2\pi r}{r^{n+1}(1-|r|)^{m}}}={\frac {M}{r^{n}(1-|r|)^{m}}}.

Dabei wird die Integrationskurve, also der Kreis mit Mittelpunkt 0 und Radius $r$ , in mathematisch positiver Richtung einfach umlaufen. Durch die spezifische Wahl von $r=1-{\tfrac {1}{n+1}}$ erhält man wegen $(1-{\tfrac {1}{n+1}})^{-n}\leq e$ insgesamt

|a_{n}|\leq Me(n+1)^{m}\leq Me2^{m}n^{m}.

Trigonometrie

Die geometrische Reihe, bzw. ihre Partialsummen, kann dabei helfen, trigonometrische Identitäten zu beweisen. In der Praxis betrifft dies zum Beispiel unmittelbar den sog. Dirichlet-Kern

D_{n}(x)=\sum _{k=-n}^{n}e^{ikx}=\left(1+2\sum _{k=1}^{n}\cos(kx)\right),

der in der Fourier-Analysis Anwendung findet.^[26] Wegen der Rechenregel $e^{ikx}=(e^{ix})^{k}$ sowie der Eulerschen Formel ergibt sich mit der geometrischen Reihe dann

\sum _{k=-n}^{n}e^{ikx}={\frac {e^{-(n+{\frac {1}{2}})ix}-e^{(n+{\frac {1}{2}})ix}}{e^{-{\frac {ix}{2}}}-e^{\frac {ix}{2}}}}={\frac {-2i\sin((n+{\frac {1}{2}})x)}{-2i\sin({\frac {x}{2}})}}={\frac {\sin((n+{\frac {1}{2}})x)}{\sin({\frac {x}{2}})}},

also die geschlossene Gestalt in Form eines Sinus-Quotienten.^[27]

Zahlentheorie

Euler-Produkte

Im Umfeld der analytischen Zahlentheorie gehört das Euler-Produkt

\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=\prod _{p\ {\text{Primzahl}}}{\frac {1}{1-{\frac {1}{p^{s}}}}}

der Riemannschen Zeta-Funktion zu den bedeutendsten Formeln, da sie die Folge der Primzahlen mit einer vergleichsweise „einfach strukturierten“ analytischen Funktion in Verbindung bringt. Dabei gelten die angegebenen Formeln jedoch nur im eingeschränkten Bereich $\mathrm {Re} (s)>1$ , wobei sich dies auf den Realteil der komplexen Zahl $s$ bezieht. Durch Ausmultiplizieren und Anwendung der geometrischen Reihe

1+{\frac {1}{p^{s}}}+{\frac {1}{p^{2s}}}+{\frac {1}{p^{3s}}}+\dotsb ={\frac {1}{1-{\frac {1}{p^{s}}}}}

mit $|p^{-s}|<1$ erkennt man für die ersten $n$ Primzahlen

{\frac {1}{1-{\frac {1}{2^{s}}}}}\cdot {\frac {1}{1-{\frac {1}{3^{s}}}}}\cdot {\frac {1}{1-{\frac {1}{5^{s}}}}}\cdot \cdots \cdot {\frac {1}{1-{\frac {1}{p_{n}^{s}}}}}=\sum _{m=2^{a_{1}}3^{a_{2}}5^{a_{3}}\cdots p_{n}^{a_{n}} \atop a_{1},a_{2},a_{3},\dots ,a_{n}\geq 0}{\frac {1}{m^{s}}}.

Nun kann man in dieser Formel $n$ gegen Unendlich laufen lassen, und erhält

\prod _{p\ {\text{Primzahl}}}{\frac {1}{1-{\frac {1}{p^{s}}}}}=\lim _{n\to \infty }\sum _{m=2^{a_{1}}3^{a_{2}}5^{a_{3}}\cdots p_{n}^{a_{n}}}{\frac {1}{m^{s}}}=\sum _{m=1}^{\infty }{\frac {1}{m^{s}}}=1+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+{\frac {1}{4^{s}}}+\cdots =\zeta (s),

da jede Zahl $m$ nach dem Fundamentalsatz der Arithmetik genau eine Zerlegung $m=2^{a_{1}}3^{a_{2}}5^{a_{3}}\cdots$ besitzt. Somit folgt das Euler-Produkt im Bereich der absoluten Konvergenz der Reihe zu $\zeta (s)$ .^[28]

Dieses Argument verallgemeinert sich auf vollständig multiplikative zahlentheoretische Funktionen $a_{n}$ (d. h. $a_{mn}=a_{m}a_{n}$ für alle $m,n$ und $a_{1}\not =0$ ) in Form der Identität

\sum _{n=1}^{\infty }a_{n}=\prod _{p\ {\text{Primzahl}}}{\frac {1}{1-a_{p}}},

die dann zutrifft, wenn die Reihe $\textstyle \sum _{n=1}^{\infty }a_{n}$ absolut konvergiert.^[29]

Satz von Weyl über Gleichverteilung

Die geometrische Reihe spielt eine wichtige Rolle bei einer kritischen Stelle im Beweis des Satzes von Weyl für Gleichverteilung. Bei diesem wird eine reelle Zahl $\alpha$ gewählt, und die Folge aller Vielfache

\alpha ,\quad 2\alpha ,\quad 3\alpha ,\quad 4\alpha ,\quad \ldots

betrachtet. Daraus kann eine Folge mit Werten in $[0,1]$ konstruiert werden mit der Gaußklammer

a_{n}(\alpha ):=n\alpha -\lfloor n\alpha \rfloor .

Der Satz von Weyl gibt eine Charakterisierung dafür, dass die Werte $a_{n}(\alpha )$ im asymptotischen Sinne im Intervall gleichverteilt ist. Dabei bedeutet „gleichverteilt“ präzise, dass für alle $0\leq a<b\leq 1$ bereits

\lim _{N\to \infty }{\frac {|\{n\in \mathbb {N} \colon a_{n}(\alpha )\in (a,b),n\leq N\}|}{N}}=b-a.

Dies trifft genau dann zu, falls $\alpha$ eine irrationale Zahl ist.^[30] Die Richtung

\alpha

rational

\implies

a_{n}(\alpha )

nicht asymptotisch gleichverteilt

kann dabei schnell gesehen werden. Für die andere Richtung zeigt man dies über das Weyl-Kriterium, das besagt, dass eine Folge $\xi _{n}\in [0,1]$ genau dann gleichverteilt ist, wenn

\lim _{N\to \infty }{\frac {1}{N}}\sum _{n=1}^{N}e^{2\pi ik\xi _{n}}=0

für alle ganzen Zahlen $k\not =0$ .^[31] Der Beweis des Weyl-Kriteriums kann mit elementarer Fourier-Analysis geführt werden.^[32] Mit der 1-Periodizität der komplexen Exponentialfunktion $e^{2\pi ix}$ erhält man für irrationale $\alpha$ über die geometrische Summenformel

{\frac {1}{N}}\sum _{n=1}^{N}e^{2\pi ika_{n}(\alpha )}={\frac {1}{N}}\sum _{n=1}^{N}e^{2\pi ik(n\alpha -\lfloor n\alpha \rfloor )}={\frac {1}{N}}\sum _{n=1}^{N}\left(e^{2\pi ik\alpha }\right)^{n}={\frac {e^{2\pi ik\alpha }}{N}}{\frac {1-e^{2\pi ik\alpha N}}{1-e^{2\pi ik\alpha }}},

wobei der letzte Ausdruck für $N\to \infty$ gegen 0 strebt.^[33]

Analytische Kombinatorik

Die geometrische Reihe findet häufige Anwendung in der analytischen Kombinatorik, zum Beispiel in der Theorie der Partitionen.^[34]

Ist $n$ eine natürliche Zahl, so ist eine absteigende Kette $\lambda _{1}\geq \lambda _{2}\geq \lambda _{3}\geq \cdots$ positiver ganzer Zahlen eine Partition von $n$ , falls

\lambda _{1}+\lambda _{2}+\lambda _{3}+\lambda _{4}+\cdots =n

gilt. Die Anzahl der Partitionen von $n$ wird mit $p(n)$ bezeichnet, und formal gilt $p(0)=1$ . Mit der geometrischen Reihe kann für die erzeugende Funktion der $p(n)$ die Produktidentität

\sum _{n=0}^{\infty }p(n)q^{n}=\prod _{n=1}^{\infty }{\frac {1}{1-q^{n}}}

gezeigt werden.^[35] Diese verbindet die Partitionsfunktion über die Dedekindsche Etafunktion mit der Theorie der Modulformen und erlaubt es unter anderem, konvergente Reihen zu konstruieren, die als Grenzwerte $p(n)$ haben.^[36] Verallgemeinern lassen sich diese Ansätze auf ähnliche Funktionen $p_{f}(n)$

\sum _{n=0}^{\infty }p_{f}(n)q^{n}=\prod _{n=1}^{\infty }{\frac {1}{(1-q^{n})^{f(n)}}},

mit Exponenten $f(n)\geq 0$ , die in verschiedensten zahlentheoretischen Kontexten auftreten.^[37]

Summierbarkeit

Eine möglicherweise nicht konvergente Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}$ heißt Abel-summierbar gegen den Grenzwert $A$ , falls die zugehörige Potenzreihe $\textstyle \sum _{n=0}^{\infty }a_{n}x^{n}$ für alle $|x|<1$ konvergiert, und ferner

\lim _{x\to 1^{-}}\sum _{n=0}^{\infty }a_{n}x^{n}=A

gilt. Abel selbst konnte zeigen, dass gewöhnliche Konvergenz von $\textstyle \sum _{n=0}^{\infty }a_{n}$ bereits Abel-Summierbarkeit impliziert, und die Grenzwerte übereinstimmen.^[38] In diesem Kontext wird die folgende Quotientenformel mit der geometrischen Reihe und $\textstyle s_{n}:=\sum _{k=0}^{n}a_{k}$ genannt,

\sum _{n=0}^{\infty }a_{n}x^{n}={\frac {\sum _{n=0}^{\infty }s_{n}x^{n}}{\sum _{n=0}^{\infty }x^{n}}},

wobei der hintere Ausdruck für $s_{n}\to A$ als ein „asymptotischer Mittelwert“ interpretiert werden kann.^[39]

Integraldarstellungen

Mit der geometrischen Reihe kann eine Integraldarstellung für die Riemannsche Zeta-Funktion gewonnen werden. Grundlage dieser Darstellung ist die eulersche Integral-Darstellung der Gamma-Funktion

\Gamma (s)=\int _{0}^{\infty }e^{-x}x^{s-1}\mathrm {d} x,

aus dem nach der Substitution $x=tn$ mit $n=1,2,3,\dotsc$ und Division durch $n^{s}$ nach beidseitigem Summieren über die geometrische Reihe der Ausdruck

\zeta (s)\Gamma (s)=\sum _{n=1}^{\infty }\int _{0}^{\infty }e^{-nt}t^{s-1}\mathrm {d} t=\int _{0}^{\infty }{\frac {t^{s-1}}{e^{t}-1}}\mathrm {d} t

hervorgeht.^[40] Diese Darstellung von $\zeta (s)\Gamma (s)$ gilt naturgemäß nur auf der Halbebene $\{s\in \mathbb {C} \colon \operatorname {Re} (s)>1\}$ . Die zweite Integraldarstellung von $\zeta (s)\Gamma (s)$ bezeichnet man auch als die Mellin-Transformation von ${\tfrac {1}{e^{t}-1}}$ . Das mögliche Vertauschen von Summe und Integral kann mit absoluter Konvergenz und dem Satz von Lebesgue begründet werden.

Verallgemeinerungen und Varianten

Endliche Summenformeln

Die Partialsumme

s_{n}=\sum _{k=0}^{n}q^{k}k

hat für

q\neq 1

das Ergebnis

s_{n}={\frac {nq^{n+2}-(n+1)q^{n+1}+q}{(q-1)^{2}}}

und für

q=1

(vgl. Gaußsche Summenformel)

s_{n}=\sum _{k=0}^{n}1^{k}k=\sum _{k=0}^{n}k={\frac {n(n+1)}{2}}

.

Die so entstehenden Werte

s_{n}

werden Dreieckszahlen genannt. Diese Formel ergibt sich auch aus der Formel für

q\neq 1

(mit zweifacher Anwendung der Regel von de L’Hospital) als deren Grenzwert für

q\to 1

.

Die Partialsumme

s_{n}=\sum _{k=0}^{n}q^{k}k^{2}

hat für

q\neq 1

das Ergebnis

s_{n}={\frac {n^{2}q^{n+3}-(2n^{2}+2n-1)q^{n+2}+(n+1)^{2}q^{n+1}-q^{2}-q}{(q-1)^{3}}}

und für

q=1

(vgl. Potenzsummen)

s_{n}={\frac {n(n+1)(2n+1)}{6}}

Die auf die nun genannte Weise entstehenden Werte

s_{n}

werden Quadratische Pyramidalzahlen genannt.

Die Dreieckszahlen und die Quadratischen Pyramidalzahlen bilden die ersten Spezialfälle zu den Faulhabersche Formeln, welche von Johannes Faulhaber entdeckt wurden.

Banach-Algebren

Die geometrische Summenformel ist sogar in jeder Banach-Algebra gültig, solange die Norm von $q$ kleiner als Eins ist; im Kontext linearer Operatoren spricht man auch von der Neumann-Reihe.

Siehe auch

Die Konvergenz bzw. Divergenz der geometrischen Reihe ist die Grundlage für das Wurzelkriterium und das Quotientenkriterium.
Geometrische Verteilung
Arithmetische Reihe
Harmonische Reihe

Literatur

Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, Basel/Boston/Berlin 2006, ISBN 978-3-7643-7755-7.
George E. Andrews: The Geometric Series in Calculus. The American Mathematical Monthly, Band 105, Nr. 1 (Jan., 1998), S. 36–40 (JSTOR:2589524)
George E. Andrews: The Theory of Partitions. Cambridge University Press, Cambridge 1984, ISBN 0-521-63766-X.
Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Springer Spektrum, Berlin/Heidelberg 2022, ISBN 978-3-662-64388-4.
Albrecht Beutelspacher: Mathe-Basics zum Studienbeginn: Survival-Kit Mathematik. Springer, 2016, S. 198–199
I. N. Bronstein, K. A. Semendjajew et al.: Taschenbuch der Mathematik. 6. Auflage. Verlag Harri Deutsch, Frankfurt am Main 2006, ISBN 978-3-8171-2006-2.
Robert B. Burckel: Classical Analysis in the Complex Plane. Birkhäuser-Verlag, New York 2021, ISBN 978-1-0716-1963-6.
Harold Edwards: Riemann’s Zeta Function. Dover Publications Inc., Mineola New York 1974, ISBN 0-486-41740-9.
Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg-Verlag, 12. Aufl. 2015, ISBN 978-3-658-11544-9.
Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer-Verlag, Berlin Heidelberg 2006, ISBN 978-3-540-31764-7.
Peter Henrici: Applied and Computational Complex Analysis. Volume 1: Power Series - Integration - Conformal Mapping - Location of Zeros. John Wiley & Sons, New York London Sydney Toronto 1974, ISBN 0-471-37244-7.
Stefan Hildebrandt: Analysis 1. Springer-Verlag, Berlin/Heidelberg 2006, ISBN 978-3-540-25368-6.
Richard Isaac: The Pleasures of Probability. Springer Verlag, New York 1995, ISBN 978-1-4612-6912-0.
Joscelyn A. Jarrett: Regular Polygons and the Geometric Series. The Mathematics Teacher, Band 75, Nr. 3 (März 1982), S. 258–261 (JSTOR:27962874)
Achim Klenke: Wahrscheinlichkeitstheorie (= Springer-Lehrbuch Masterclass.). 3., überarbeitete und ergänzte Auflage, Springer Spektrum, Berlin/Heidelberg 2013, ISBN 978-3-642-36018-3.
Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Springer-Verlag, Berlin u. a. 1996, ISBN 3-540-59111-7.
Jacob Korevaar: Tauberian Theory. A Century of Developments. Springer-Verlag, Berlin Heidelberg New York 2004, ISBN 3-540-21058-X.
Serge Lang: A First Course in Calculus. Fifth Edition, Springer-Verlag, New York 1986, ISBN 0-387-96201-8.
Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer-Verlag, Heidelberg 2002, ISBN 3-540-41855-5.
Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton University Press, Princeton New Jersey 2003, ISBN 978-0-691-11384-5.
John Stillwell: Mathematics and Its History. Third Edition, Springer-Verlag, New York / Dordrecht / Heidelberg / London 2010, ISBN 978-1-4419-6052-8.
Terence Tao: Analysis I. Third Edition, Hindustan Book Agency, New Delhi 2017, ISBN 978-93-80250-64-9.
Guido Walz (Hrsg.): Lexikon der Mathematik. Band 2. 2. Auflage, Springer-Verlag, Heidelberg 2017, ISBN 978-3-662-53503-5.

Weblinks

Commons: Geometric series – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Mathe für Nicht-Freaks: Geometrische Reihe – Lern- und Lehrmaterialien

Wikibooks: Mathe für Nicht-Freaks: Geometrische Summenformel – Lern- und Lehrmaterialien

Eric W. Weisstein: Geometric Series. In: MathWorld (englisch).
Geometrische Folgen und Reihen auf mathematische-basteleien.de
Unendliche geometrische Reihe, Archivlink, abgerufen am 8. März 2022

Einzelnachweise

↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Basel/Boston/Berlin 2006, S. 196.
↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Basel/Boston/Berlin 2006, S. 196–197.
↑ Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 180
↑ Mathematics Magazine, vol. 72, no. 1 (Feb. 1999), S. 63
↑ Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 186
↑ Mathematics Magazine, vol. 62, no. 5 (Dec. 1989), S. 332–333.
↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 180–181.
↑ vgl. Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Basel/Boston/Berlin 2006, S. 200.
↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Basel/Boston/Berlin 2006, S. 200–201.
↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Basel/Boston/Berlin 2006, S. 204.
↑ Vergleiche Achim Klenke: Wahrscheinlichkeitstheorie. Berlin/Heidelberg 2013, S. 12.
↑ Achim Klenke: Wahrscheinlichkeitstheorie. Berlin/Heidelberg 2013, S. 44–45.
↑ Richard Isaac: The Pleasures of Probability. New York 1995, S. 104.
↑ Richard Isaac: The Pleasures of Probability. New York 1995, S. 107.
↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Berlin Heidelberg 2006, S. 104.
↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 218.
↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 219.
↑ Robert B. Burckel: Classical Analysis in the Complex Plane. New York 2021, S. 127–128.
↑ Peter Henrici: Applied and Computational Complex Analysis. Volume 1: Power Series - Integration - Conformal Mapping - Location of Zeros. New York London Sydney Toronto 1974, S. 569.
↑ Peter Henrici: Applied and Computational Complex Analysis. Volume 1: Power Series - Integration - Conformal Mapping - Location of Zeros. New York London Sydney Toronto 1974, S. 570.
↑ Peter Henrici: Applied and Computational Complex Analysis. Volume 1: Power Series - Integration - Conformal Mapping - Location of Zeros. New York London Sydney Toronto 1974, S. 570–571.
↑ Peter Henrici: Applied and Computational Complex Analysis. Volume 1: Power Series - Integration - Conformal Mapping - Location of Zeros. New York London Sydney Toronto 1974, S. 584–586.
↑ Peter Henrici: Applied and Computational Complex Analysis. Volume 1: Power Series - Integration - Conformal Mapping - Location of Zeros. New York London Sydney Toronto 1974, S. 587.
↑ ^a ^b Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 189.
↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 190.
↑ Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 44–45.
↑ Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 37.
↑ Harold Edwards: Riemann’s Zeta Function. Mineola New York 1974, S. 6–7.
↑ Tom M. Apostol: Introduction to Analytic Number Theory. New York 1976, S. 230.
↑ Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 107.
↑ Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 112.
↑ Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 106–111.
↑ Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 109.
↑ George E. Andrews: The Theory of Partitions. Cambridge 1984, S. 4, 24–25, 126, 188.
↑ George E. Andrews: The Theory of Partitions. Cambridge 1984, S. 4.
↑ George E. Andrews: The Theory of Partitions. Cambridge 1984, S. 68–81.
↑ Walter Bridges, Benjamin Brindle, Kathrin Bringmann, und Johann Franke: Asymptotic expansions for partitions generated by infinite products. Mathematische Annalen, 2024.
↑ Jacob Korevaar: Tauberian Theory. A Century of Developments. Berlin Heidelberg New York 2004, S. 4.
↑ Jacob Korevaar: Tauberian Theory. A Century of Developments. Berlin Heidelberg New York 2004, S. 1.
↑ T. M. Apostol: Introduction to Analytic Number Theory. New York / Heidelberg / Berlin 1976, S. 251.

[1] Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Basel/Boston/Berlin 2006, S. 196.

[2] Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Basel/Boston/Berlin 2006, S. 196–197.

[3] Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 180

[4] Mathematics Magazine, vol. 72, no. 1 (Feb. 1999), S. 63

[5] Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 186

[6] Mathematics Magazine, vol. 62, no. 5 (Dec. 1989), S. 332–333.

[7] Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 180–181.

[8] vgl. Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Basel/Boston/Berlin 2006, S. 200.

[9] Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Basel/Boston/Berlin 2006, S. 200–201.

[10] Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Basel/Boston/Berlin 2006, S. 204.

[11] Vergleiche Achim Klenke: Wahrscheinlichkeitstheorie. Berlin/Heidelberg 2013, S. 12.

[12] Achim Klenke: Wahrscheinlichkeitstheorie. Berlin/Heidelberg 2013, S. 44–45.

[13] Richard Isaac: The Pleasures of Probability. New York 1995, S. 104.

[14] Richard Isaac: The Pleasures of Probability. New York 1995, S. 107.

[15] Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Berlin Heidelberg 2006, S. 104.

[16] Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 218.

[17] Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 219.

[18] Robert B. Burckel: Classical Analysis in the Complex Plane. New York 2021, S. 127–128.

[19] Peter Henrici: Applied and Computational Complex Analysis. Volume 1: Power Series - Integration - Conformal Mapping - Location of Zeros. New York London Sydney Toronto 1974, S. 569.

[20] Peter Henrici: Applied and Computational Complex Analysis. Volume 1: Power Series - Integration - Conformal Mapping - Location of Zeros. New York London Sydney Toronto 1974, S. 570.

[21] Peter Henrici: Applied and Computational Complex Analysis. Volume 1: Power Series - Integration - Conformal Mapping - Location of Zeros. New York London Sydney Toronto 1974, S. 570–571.

[22] Peter Henrici: Applied and Computational Complex Analysis. Volume 1: Power Series - Integration - Conformal Mapping - Location of Zeros. New York London Sydney Toronto 1974, S. 584–586.

[23] Peter Henrici: Applied and Computational Complex Analysis. Volume 1: Power Series - Integration - Conformal Mapping - Location of Zeros. New York London Sydney Toronto 1974, S. 587.

[RS189-24] Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 189.

[RS190-25] Reinhold Remmert, Georg Schumacher: Funktionentheorie 1, 5. Auflage, Springer, S. 190.

[26] Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 44–45.

[27] Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 37.

[28] Harold Edwards: Riemann’s Zeta Function. Mineola New York 1974, S. 6–7.

[29] Tom M. Apostol: Introduction to Analytic Number Theory. New York 1976, S. 230.

[30] Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 107.

[31] Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 112.

[32] Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 106–111.

[33] Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 109.

[34] George E. Andrews: The Theory of Partitions. Cambridge 1984, S. 4, 24–25, 126, 188.

[35] George E. Andrews: The Theory of Partitions. Cambridge 1984, S. 4.

[36] George E. Andrews: The Theory of Partitions. Cambridge 1984, S. 68–81.

[37] Walter Bridges, Benjamin Brindle, Kathrin Bringmann, und Johann Franke: Asymptotic expansions for partitions generated by infinite products. Mathematische Annalen, 2024.

[38] Jacob Korevaar: Tauberian Theory. A Century of Developments. Berlin Heidelberg New York 2004, S. 4.

[39] Jacob Korevaar: Tauberian Theory. A Century of Developments. Berlin Heidelberg New York 2004, S. 1.

[40] T. M. Apostol: Introduction to Analytic Number Theory. New York / Heidelberg / Berlin 1976, S. 251.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

Geometrische Reihe

Definition

Konvergenzkriterium

Zahlenbeispiel

Geometrische Veranschaulichungen

Zur Summenformel

Zu einer verwandten Summenformel

Geschichte

Bei Zenon von Elea

Teilungsparadoxon

Achilles und die Schildkröte

Anwendungen

Rentenrechnung

Periodische Dezimalbrüche

Wahrscheinlichkeitstheorie

Geometrische Verteilung

Ruin des Spielers

Fraktale Geometrie

Harmonische Reihe

Funktionentheorie

Als Majorante

Explizite Taylor-Reihen

Cauchyscher Entwicklungssatz

Abschätzung von Taylor-Koeffizienten

Trigonometrie

Zahlentheorie

Euler-Produkte

Satz von Weyl über Gleichverteilung

Analytische Kombinatorik

Summierbarkeit

Integraldarstellungen

Verallgemeinerungen und Varianten

Endliche Summenformeln

Verwandte Potenzreihen und spezielle Funktionen

Banach-Algebren

Siehe auch

Literatur

Weblinks

Einzelnachweise

What are your Feelings

Share This Article :